已知函数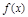 =x2-4x+a+3,g(x)=mx+5-2m.
=x2-4x+a+3,g(x)=mx+5-2m.
(Ⅰ)若方程f(x)=0在[-1,1]上有实数根,求实数a的取值范围;
(Ⅱ)当a=0时,若对任意的x1∈[1,4],总存在x2∈[1,4],使f(x1)=g(x2)成立,求实数m的取值范围;
(Ⅲ)若函数y=f(x)(x∈[t,4])的值域为区间D,是否存在常数t,使区间D的长度为7-2t?若存在,求出t的值;若不存在,请说明理由(注:区间[p,q]的长度为q-p).
给定可导函数 ,如果存在
,如果存在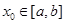 ,使得
,使得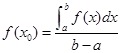 成立,则称
成立,则称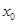 为函数
为函数 在区间
在区间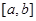 上的“平均值点”.
上的“平均值点”.
(1)函数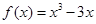 在区间
在区间 上的平均值点为;
上的平均值点为;
(2)如果函数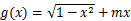 在区间
在区间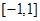 上有两个“平均值点”,则实数
上有两个“平均值点”,则实数 的取值范围是.
的取值范围是.
已知函数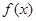 是
是 上的减函数,且
上的减函数,且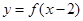 的图象关于点
的图象关于点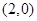 成中心对称.若
成中心对称.若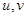 满足不等式组
满足不等式组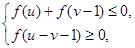 则
则 的最小值为.
的最小值为.
已知函数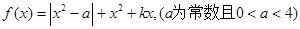 。
。
(1)若 ,求不等式
,求不等式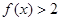 的解集;
的解集;
(2)若函数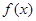 在
在 上有两个零点
上有两个零点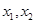 ,求
,求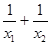 的取值范围.
的取值范围.
已知抛物线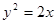 上有四点
上有四点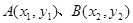 、
、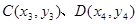 ,点M(3,0),直线AB、CD都过点M,且都不垂直于x轴,直线PQ过点M且垂直于x轴,交AC于点P,交BD于点Q.
,点M(3,0),直线AB、CD都过点M,且都不垂直于x轴,直线PQ过点M且垂直于x轴,交AC于点P,交BD于点Q.
(1)求 的值;
的值;
(2)求证: .
.
在四棱锥 中,底面
中,底面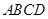 为直角梯形,
为直角梯形,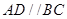 ,
,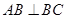 侧面
侧面 底面
底面 ,
,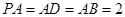 ,
, .
.
(1)若 中点为
中点为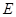 .求证:
.求证: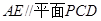 ;
;
(2)若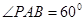 ,求直线
,求直线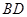 与平面
与平面 所成角的正弦值.
所成角的正弦值.