给定可导函数 ,如果存在
,如果存在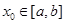 ,使得
,使得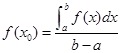 成立,则称
成立,则称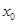 为函数
为函数 在区间
在区间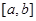 上的“平均值点”.
上的“平均值点”.
(1)函数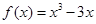 在区间
在区间 上的平均值点为;
上的平均值点为;
(2)如果函数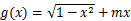 在区间
在区间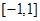 上有两个“平均值点”,则实数
上有两个“平均值点”,则实数 的取值范围是.
的取值范围是.
青少年“心理健康”问题越来越引起社会关注,某校对高一600名学生进行了一次“心理健康”知识测试,并从中抽取了部分学生的成绩(得分取正整数,满分100分)作为样本,绘制了下面尚未完成的频率分布表和频率分布直方图.
(1)填写答题卡频率分布表中的空格,补全频率分布直方图,并标出每个小矩形对应的纵轴数据;
(2)试估计该年段成绩在[70,90)段的有多少人;
(3)请你估算该年段的平均分.
若tan(π-α)=2,求2sin(3π+α)·cos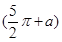 +sin
+sin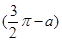 ·sin(π-α)的值
·sin(π-α)的值
已知奇函数f(x)=
(1)求实数m的值,并在给出的直角坐标系中画出y=f(x)的图象;
(2)若函数f(x)在区间[-1,a-2]上单调递增,试确定a的取值范围.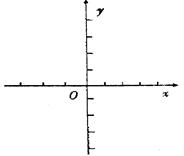
已知函数 .
.
(Ⅰ)当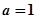 时,求函数
时,求函数 的单调区间;
的单调区间;
(Ⅱ)若函数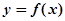 的图像在点
的图像在点 处的切线的倾斜角为
处的切线的倾斜角为 ,问:m在什么范围取值时,对于任意的
,问:m在什么范围取值时,对于任意的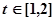 ,函数
,函数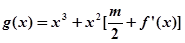 在区间
在区间 上总存在极值?
上总存在极值?
(Ⅲ)当 时,设函数
时,设函数 ,若在区间
,若在区间 上至少存在一个
上至少存在一个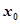 ,使得
,使得 成立,试求实数p的取值范围.
成立,试求实数p的取值范围.
已知数列 的前
的前 项和为
项和为 ,满足
,满足 ,且
,且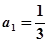 .
.
(Ⅰ)求 ,
, ,
, ;
;
(Ⅱ)猜想数列 的通项公式,并用数学归纳法加以证明.
的通项公式,并用数学归纳法加以证明.