在四棱锥 中,底面
中,底面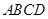 为直角梯形,
为直角梯形,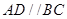 ,
,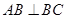 侧面
侧面 底面
底面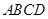 ,
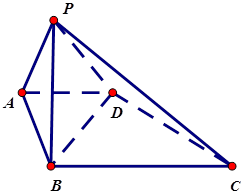
,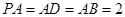 ,
, .
.
(1)若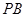 中点为
中点为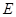 .求证:
.求证: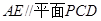 ;
;
(2)若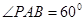 ,求直线
,求直线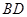 与平面
与平面 所成角的正弦值.
所成角的正弦值.
已知函数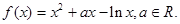
(I)若函数 在
在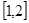 上是减函数,求实数
上是减函数,求实数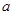 的取值范围;
的取值范围;
(II)令 ,是否存在实数
,是否存在实数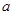 ,当
,当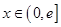 (
(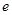 是自然常数)时,函数
是自然常数)时,函数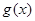 的最小值
的最小值
是3,若存在,求出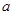 的值;若不存在,说明理由;
的值;若不存在,说明理由;
(Ⅲ)当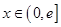 时,证明:
时,证明: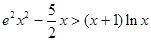 .
.
(本小题满分14分)
设椭圆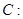
 的离心率为
的离心率为 =
=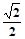 ,点
,点 是椭圆上的一点,且点
是椭圆上的一点,且点 到椭圆
到椭圆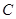 两焦点的距离之和为4.
两焦点的距离之和为4.
(1)求椭圆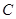 的方程;
的方程;
(2)椭圆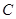 上一动点
上一动点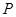
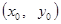 关于直线
关于直线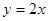 的对称点为
的对称点为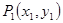 ,求
,求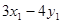 的取值范围.
的取值范围.
如图1,在直角梯形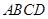 中,
中,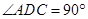 ,
, ,
,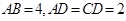 ,
,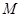 为线段
为线段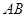 的中点.将
的中点.将 沿
沿 折起,使平面
折起,使平面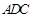
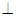 平面
平面 ,得到几何体
,得到几何体 ,如图2所示.
,如图2所示.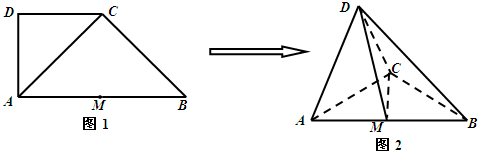
(Ⅰ)求证: 平面
平面 ;
;
(Ⅱ)求二面角 的余弦值.
的余弦值.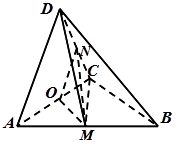
为了解高中一年级学生身高情况,某校按10%的比例对全校700名高中一年级学生按性别
进行抽样检查,测得身高频数分布表如下表1、表2.
表1:男生身高频数分布表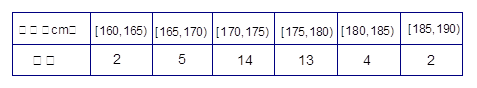
表2:女生身高频数分布表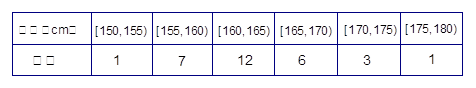
(1)求该校男生的人数并完成下面频率分布直方图;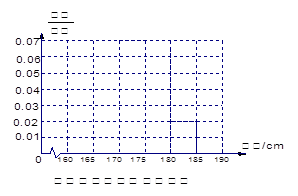
(2)估计该校学生身高(单位:cm)在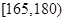 的概率;
的概率;
(3)在男生样本中,从身高(单位:cm)在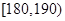 的男生中任选3人,设
的男生中任选3人,设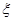 表示所选3人中身高(单位:cm)在
表示所选3人中身高(单位:cm)在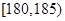 的人数,求
的人数,求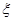 的分布列和数学期望.
的分布列和数学期望.
(本小题满分10分)选修4-5:不等式选讲
设函数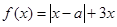 ,其中
,其中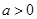 .
.
(Ⅰ)当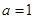 时,求不等式
时,求不等式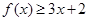 的解集;
的解集;
(Ⅱ)若不等式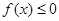 的解集为
的解集为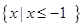 ,求a的值.
,求a的值.