已知：在△ABC中，∠ACB=90°，CD⊥AB于点D，点E在AC上，BE交CD于点G，EF⊥BE交AB于点F．如图甲，当AC=BC，且CE=EA时，则有EF=EG；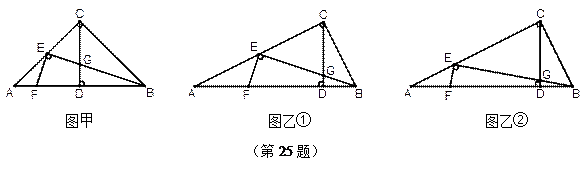
（1）如图乙①，当AC=2BC，且CE=EA时，则线段EF与EG的数量关系是：EF EG；
（2）如图乙②，当AC=2BC，且CE=2EA时，请探究线段EF与EG的数量关系，并证明你的结论；
（3）当AC=mBC，且CE=nEA时，请探究线段EF与EG的数量关系，直接写出你的结论（不必证明）．
请在下图方格中任画出两个以AB腰的等腰三角形ABC。（要求：一个为锐角三角形，一个为钝角三角形）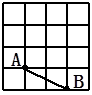
解下列不等式及不等式组：(本题共8分,每题3分，数轴2分)
(1) 2－4x＜0 (2)解不等式组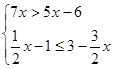
，并把解集在数轴上表示出来。
如图，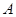
是半径为
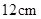的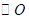
上的定点，动点
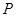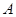从出发，以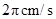
的速度沿圆周逆时针运动，当点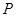回到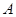地立即停止运动．
（1）如果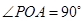
，求点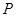运动的时间；
（2）如果点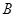
是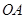
延长线上的一点，
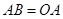，那么当点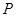运动的时间为
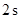时，判断直线
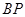与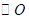的位置关系，并说明理由．
为实现区域教育均衡发展，我市计划对某县
、
两类薄弱学校全部进行改造．根据预算，共需资金1575万元．改造一所类学校和两所类学校共需资金230万元；改造两所类学校和一所类学校共需资金205万元．
（1）改造一所类学校和一所类学校所需的资金分别是多少万元？
（2）若该县的类学校不超过5所，则类学校至少有多少所？
（3）我市计划今年对该县、两类学校共6所进行改造，改造资金由国家财政和地方财政共同承担．若今年国家财政拨付的改造资金不超过400万元；地方财政投入的改造资金不少于70万元，其中地方财政投入到、两类学校的改造资金分别为每所10万元和15万元．请你通过计算求出有几种改造方案？
某足球协会举办了一次足球联赛，记分规则是：胜一场得3分，平一场得1分，负一场得0分.当比赛进行到12轮结束（每队均需比赛12场）时，甲队得分是19分，请你通过计算分析甲队胜几场、平几场、负几场？