如图,某幢大楼的外墙边上竖直安装着一根旗杆 ,小明在离旗杆下方大楼底部
,小明在离旗杆下方大楼底部 点24米的点
点24米的点 处放置一台测角仪,测角仪的高度
处放置一台测角仪,测角仪的高度 为1.5米,并在点
为1.5米,并在点 处测得旗杆下端
处测得旗杆下端 的仰角为40°,上端
的仰角为40°,上端 的仰角为45°,求旗杆
的仰角为45°,求旗杆 的长度;(结果精确到0.1米,参考数据:
的长度;(结果精确到0.1米,参考数据: ,
, ,
, )
)
学习与探究
(1)请在图1的正方形 内,作出使
内,作出使 的所有点
的所有点 ,并简要说明作法.
,并简要说明作法.
我们可以这样解决问题:利用直径所对的圆周角等于90°,作以AB为直径的圆,则正方形ABCD内部的半圆上所有点(A、B除外)为所求.
(2)请在图2的正方形 内(含边),画出使
内(含边),画出使 的所有的点
的所有的点 ,尺规作图,不写作法,保留痕迹;
,尺规作图,不写作法,保留痕迹;
(3)如图3,已知矩形ABCD中,AB=4,BC=3,请在矩形内(含边),画出 的所有的点
的所有的点 ,尺规作图,不写作法,保留痕迹.
,尺规作图,不写作法,保留痕迹.
已知二次函数y=x2-(2a+3)x+4a+2与x轴交于A、B两点,与y轴交于点C,并且点A在点B左侧,位于原点两侧. 若S△ABC的面积为3,求a的值.
在图1、图2中,线段AC=CE,点B是线段AC的中点,点D是线段CE的中点.四边形BCGF和CDHN都是正方形.AE的中点是M.
如图1,点E在AC的延长线上,点N与点G重合时,点M与点C重合,容易证明FM = MH,FM⊥HM;现将图1中的CE绕点C顺时针旋转一个锐角,得到图2,判断△FMH的形状,并证明你的结论.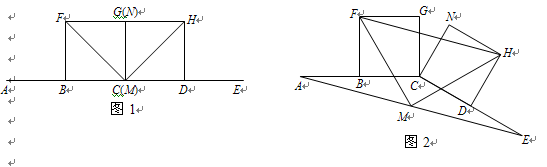
某数码卖场销售某种品牌电脑,对于100~500台的大客户订单实行降价促销,每台电脑的售价y(元/台)与数量x(台)的函数关系可以由图中线段AB来表示,每台电脑的进货及运输等成本总共为2250元。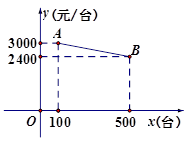
(1)写出每台电脑的售价y与台数x的函数关系式:________________;自变量的取值范围是____________且x为整数;
(2)若一次政府采购的订单使该卖场共获利12万元,不计其它成本消耗,试求出这次政府采购了多少台电脑;
(3)求出每份大客户订单的总获利z(元)与购买数量x(台)之间的函数关系式。当一份订单的购买数量为多少台时,卖场获利最多?
如图,已知△ABC内接于⊙O,∠BAC=60°,AD⊥BC于D,BE⊥AC于E交AD于H,若CF是⊙O的直径,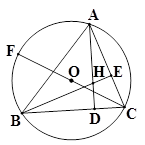
(1)求∠FCB的度数;
(2)求证:AH=
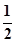 CF.
CF.