已知二次函数y=x2-(2a+3)x+4a+2与x轴交于A、B两点,与y轴交于点C,并且点A在点B左侧,位于原点两侧. 若S△ABC的面积为3,求a的值.
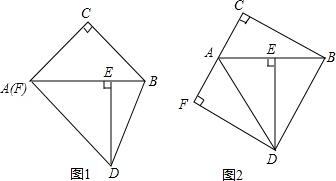
在 中, , 绕点 顺时针旋转到 的位置,点 在斜边 上,连接 ,过点 作 于点 .
(1)如图1,若点 与点 重合,求证: ;
(2)若 ,
①如图2,当点 在线段 的延长线上时,判断线段 与线段 的数量关系,并说明理由;
②当点 在线段 上时,设 ,请用含 的代数式表示线段 .
如图,“中国海监50”正在南海海域 处巡逻,岛礁 上的中国海军发现点 在点 的正西方向上,岛礁 上的中国海军发现点 在点 的南偏东 方向上,已知点 在点 的北偏西 方向上,且 、 两地相距120海里.
(1)求出此时点 到岛礁 的距离;
(2)若“中海监50”从 处沿 方向向岛礁 驶去,当到达点 时,测得点 在 的南偏东 的方向上,求此时“中国海监50”的航行距离.(注 结果保留根号)
如图,在平行四边形 中,点 、 、 的坐标分别是 、 、 ,双曲线 过点 .
(1)求双曲线的解析式;
(2)作直线 交 轴于点 ,连接 ,求 的面积.
如图,在 中,点 是直径 延长线上一点,过点 作 的切线,切点为 ,连接 .
(1)求证: ;
(2)若 平分 ,且分别交 、 于点 、 ,当 时,求 的长.

某大型企业为了保护环境,准备购买 、 两种型号的污水处理设备共8台,用于同时治理不同成分的污水,若购买 型2台、 型3台需54万,购买 型4台、 型2台需68万元.
(1)求出 型、 型污水处理设备的单价;
(2)经核实,一台 型设备一个月可处理污水220吨,一台 型设备一个月可处理污水190吨,如果该企业每月的污水处理量不低于1565吨,请你为该企业设计一种最省钱的购买方案.