(本小题满分12分)
为了预防春季流感，市防疫部门提供了编号为1，2，3，4 的四种疫苗供市民选择注射，每个人均能从中任选一个编号的疫苗接种，现在甲，乙，丙三人接种疫苗
（I）求三人注射的疫苗编号互不相同的概率
（II）求三人中至少有一人选 1号疫苗的概率
已知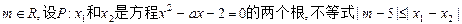
对任意实数
恒成立；Q：函数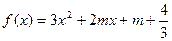
有两个不同的零点. 求使“P∧Q”为真命题的实数m的取值范围.
在△ABC中，角A，B，C所对的边分别为a，b，c.已知
，且满足
.
(1)求角A的大小；
(2)若||＋||＝||，试判断△ABC的形状．
14分）已知椭圆中心在原点，焦点在x轴上，一个顶点为A（0，－1），且其右焦点到直线x－y＋
=0的距离为3．（I）求椭圆的方程；
（II）是否存在斜率为k（k≠0）的直线l，使l与已知椭圆交于不同的两点M、N，
且|AN|＝|AM|？若存在，求出k的取值范围；若不存在，请说明理由．
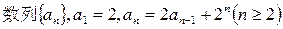
（I）求证数列
；
（II）求数列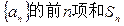
；
（III）
。
设函数
为奇函数，其图象在x=1处的切线与直线
垂直，导函数
的最小值为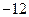
．
（I）求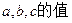
；
（II）求函数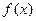
的单调递增区间，并求函数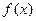在
上的最大值和最小值．