设椭圆 :
: 的左、右焦点分别为
的左、右焦点分别为 ,上顶点为
,上顶点为 ,过点
,过点 与
与 垂直的直线交
垂直的直线交 轴负半轴于点
轴负半轴于点 ,且
,且 .
.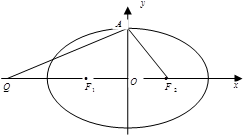
(1)求椭圆 的离心率;
的离心率;
(2)若过 、
、 、
、 三点的圆恰好与直线
三点的圆恰好与直线 :
: 相切,求椭圆
相切,求椭圆 的方程;
的方程;
(3)在(2)的条件下,过右焦点 作斜率为
作斜率为 的直线
的直线 与椭圆
与椭圆 交于
交于 、
、 两点,在
两点,在 轴上是否存在点
轴上是否存在点 使得以
使得以 为邻边的平行四边形是菱形,如果存在,求出
为邻边的平行四边形是菱形,如果存在,求出 的取值范围,如果不存在,说明理由.
的取值范围,如果不存在,说明理由.
下面有两个关于“袋子中装有红、白两种颜色的相同小球,从袋中无放回地取球”的游戏规则,这两个游戏规则公平吗?为什么?
| 游 戏 1 |
游 戏 2 |
| 2个红球和2个白球 |
3个红球和1个白球 |
| 取1个球,再取1个球 |
取1个球,再取1个球 |
| 取出的两个球同色→甲胜 |
取出的两个球同色→甲胜 |
| 取出的两个球不同色→乙胜 |
取出的两个球不同色→乙胜 |
从某小学随机抽取100名学生,将他们的身高(单位:厘米)按照区间 [ 100 , 110),[ 110 , 120),[ 120 , 130),[130 ,140) , [140 , 150]进行分组,得到频率分布直方图(如图).
(Ⅰ)求直方图中a的值;
(Ⅱ)若要从身高在[ 120 , 130),[130 ,140) , [140 , 150] 三组内的学生中,用分层抽样的方法选取18人参加一项活动,求从身高在[140 ,150]内的学生中应选取的人数;
(Ⅲ)这100名学生的平均身高约为多少厘米?
选修4-5:不等式选讲
关于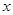 的不等式
的不等式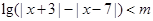 .
.
(1)当 时,解此不等式;
时,解此不等式;
(2)设函数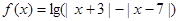 ,当
,当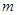 为何值时,
为何值时, 恒成立?
恒成立?
选修4-4:坐标系与参数方程
已知直线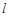 的参数方程是
的参数方程是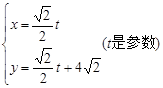 ,圆C的极坐标方程为
,圆C的极坐标方程为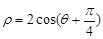 .
.
(1)求圆心C的直角坐标;
(2)由直线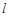 上的点向圆C引切线,求切线长的最小值.
上的点向圆C引切线,求切线长的最小值.
选修4-1:几何证明选讲
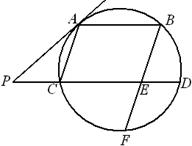
如图,AB、CD是圆的两条平行弦,BE//AC,BE交CD于E、交圆于F,过A点的切线交DC的延长线于P,PC=ED=1,PA=2.
(1)求AC的长;
(2)求证:BE=EF.