(本小题满分12分)
为了预防春季流感,市防疫部门提供了编号为1,2,3,4的四种疫苗供市民选择注射,每个人均能从中任选一个编号的疫苗接种,现有甲,乙,丙三人接科苗.
(I )求三人注射的疫苗编号互不相同的概率;
(II)设三人中选择的疫苗编号最大数为 ,求
,求 的分布列及数学期望.
的分布列及数学期望.
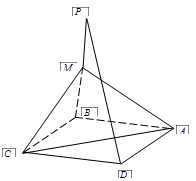
如图,已知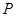 为平行四边形
为平行四边形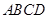 所在平面外一点,
所在平面外一点,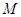 为
为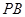 的中点,
的中点,
求证: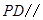 平面
平面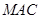 .
.
△ABC中, ,求
,求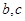 。
。
已知a=3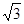 ,c=2,B=150°,求边b的长及S△.
,c=2,B=150°,求边b的长及S△.
设函数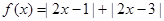 ,
,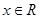 .
.
(1)解不等式: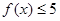 ;
;
(2)若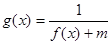 的定义域为
的定义域为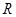 ,求实数
,求实数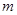 的取值范围.
的取值范围.
定义:如果数列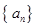 的任意连续三项均能构成一个三角形的三边长,则称
的任意连续三项均能构成一个三角形的三边长,则称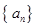 为“三角形”数列.对于“三角形”数列
为“三角形”数列.对于“三角形”数列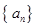 ,如果函数
,如果函数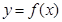 使得
使得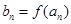 仍为一个“三角形”数列,则称
仍为一个“三角形”数列,则称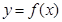 是数列
是数列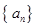 的“保三角形函数”,
的“保三角形函数”,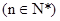 .
.
(Ⅰ)已知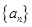 是首项为2,公差为1的等差数列,若
是首项为2,公差为1的等差数列,若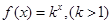 是数列
是数列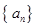 的“保三角形函数”,求k的取值范围;
的“保三角形函数”,求k的取值范围;
(Ⅱ)已知数列 的首项为2010,
的首项为2010,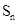 是数列
是数列 的前n项和,且满足
的前n项和,且满足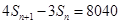 ,证明
,证明 是“三角形”数列;
是“三角形”数列;
(Ⅲ)根据“保三角形函数”的定义,对函数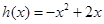 ,
,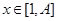 ,和数列1,
,和数列1,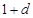 ,
,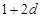 ,(
,( )提出一个正确的命题,并说明理由.
)提出一个正确的命题,并说明理由.