定义:如果数列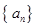 的任意连续三项均能构成一个三角形的三边长,则称
的任意连续三项均能构成一个三角形的三边长,则称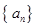 为“三角形”数列.对于“三角形”数列
为“三角形”数列.对于“三角形”数列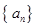 ,如果函数
,如果函数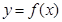 使得
使得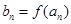 仍为一个“三角形”数列,则称
仍为一个“三角形”数列,则称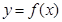 是数列
是数列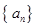 的“保三角形函数”,
的“保三角形函数”,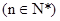 .
.
(Ⅰ)已知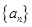 是首项为2,公差为1的等差数列,若
是首项为2,公差为1的等差数列,若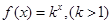 是数列
是数列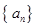 的“保三角形函数”,求k的取值范围;
的“保三角形函数”,求k的取值范围;
(Ⅱ)已知数列 的首项为2010,
的首项为2010,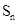 是数列
是数列 的前n项和,且满足
的前n项和,且满足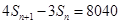 ,证明
,证明 是“三角形”数列;
是“三角形”数列;
(Ⅲ)根据“保三角形函数”的定义,对函数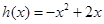 ,
,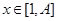 ,和数列1,
,和数列1,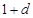 ,
,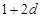 ,(
,( )提出一个正确的命题,并说明理由.
)提出一个正确的命题,并说明理由.
已知 ,动点
,动点 满足
满足 .
.
(Ⅰ)求动点 的轨迹
的轨迹 的方程;
的方程;
(Ⅱ)过点 作直线
作直线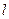 与曲线
与曲线 交于
交于 两点,若
两点,若 ,求直线
,求直线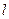 的方程;
的方程;
(Ⅲ)设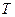 为曲线
为曲线 在第一象限内的一点,曲线
在第一象限内的一点,曲线 在
在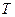 处的切线与
处的切线与
 轴分别交于点
轴分别交于点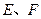 ,求
,求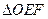 面积的最小值.
面积的最小值.
已知抛物线y=x2上的两点A、B满足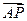 =l
=l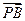 ,l>0,其中点P坐标为(0,1),
,l>0,其中点P坐标为(0,1), =
= +
+ ,O为坐标原点.
,O为坐标原点.
(I)求四边形OAMB的面积的最小值;
(II)求点M的轨迹方程.
设A,B分别是直线 和
和 上的两个动点,并且
上的两个动点,并且 ,动点P满足
,动点P满足 .记动点P的轨迹为C.
.记动点P的轨迹为C.
(I)求轨迹C的方程;
(II)若点D的坐标为(0,16),M、N是曲线C上的两个动点,且 ,求实数
,求实数 的取值范围.
的取值范围.
已知A.B是椭圆 上两点,O是坐标原点,定点
上两点,O是坐标原点,定点 ,向量
,向量 .
. 在向量
在向量 方向上的投影分别是m.n ,且
方向上的投影分别是m.n ,且 7mn ,动点P满足
7mn ,动点P满足
(Ⅰ)求点P的轨迹C的方程;
(Ⅱ)设过点E的直线l与C交于两个不同的点M.N,求 的取值范围。
的取值范围。
已知点P与定点F 的距离和它到定直线l:
的距离和它到定直线l: 的距离之比是1 : 2.
的距离之比是1 : 2.
(1)求点P的轨迹C方程;
(2)过点F的直线交曲线C于A, B两点, A, B在l上的射影分别为M, N.
求证AN与BM的公共点在x轴上.