(本小题12分)
已知动点P到定点A(0,1)的距离比它到定直线y = -2的距离小1.
(I)求动点P的轨迹C的方程;
(II)已知点Q为直线y= -1上的动点,过点q作曲线C的两条切线,切点分别为M,N,求 的取值范围.(其中O为坐标原点)
的取值范围.(其中O为坐标原点)
(本小题共13分)
已知函数 .
.
(I)求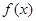 的最小正周期;(II)求
的最小正周期;(II)求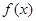 在区间
在区间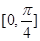 上的取值范围.
上的取值范围.
在锐角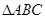 中,
中,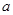 ,
,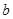 ,
,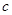 分别为内角
分别为内角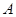 ,
,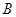 ,
,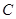 所对的边,且满足
所对的边,且满足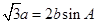 .
.
(Ⅰ)求角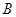 的大小;
的大小;
(Ⅱ)若 ,且
,且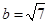 ,求
,求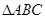 的面积。
的面积。
(本小题满分14分)已知函数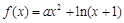 .
.
(Ⅰ)当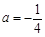 时,求函数
时,求函数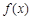 的单调区间;
的单调区间;
(Ⅱ)当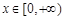 时,函数
时,函数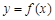 图象上的点都在
图象上的点都在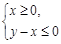 所表示的平面区域内,求实数a的取值范围.
所表示的平面区域内,求实数a的取值范围.
(Ⅲ)求证: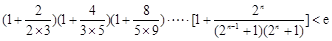 (其中
(其中 ,e是自然对数的底数).
,e是自然对数的底数).
(本小题满分12分) 设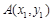 、
、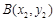 是函数
是函数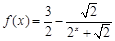 图象上任意两点,且
图象上任意两点,且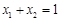 .
.
(Ⅰ)求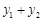 的值;
的值;
(Ⅱ)若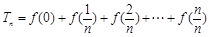 (其中
(其中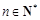 ),求
),求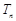 ;
;
(Ⅲ)在(Ⅱ)的条件下,设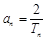 (
(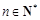 ),若不等式
),若不等式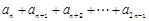 >
>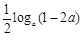 对任意的正整数n恒成立,求实数a的取值范围.
对任意的正整数n恒成立,求实数a的取值范围.
(本小题满分12分) 已知函数 (
(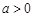 且
且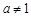 )的图象过点
)的图象过点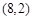 ,点
,点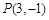 关于直线
关于直线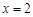 的对称点
的对称点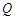 在
在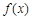 的图象上.
的图象上.
(Ⅰ)求函数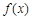 的解析式;
的解析式;
(Ⅱ)令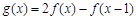 ,求
,求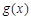 的最小值及取得最小值时x的值.
的最小值及取得最小值时x的值.