(本小题满分12分)
一项试验有两套方案,每套方案试验成功的概率都是 ,试验不成功的概率都是
,试验不成功的概率都是 甲随机地从两套方案中选取一套进行这项试验,共试验了 3次,每次实验相互独立,且要从两套方案中等可能地选择一套.
甲随机地从两套方案中选取一套进行这项试验,共试验了 3次,每次实验相互独立,且要从两套方案中等可能地选择一套.
(I)求3次试验都选择了同一套方案且都试验成功的概率:(II)记3次试验中,都选择了第一套方案并试难成功的次数为X,求X的分布列和期望EX.
设函数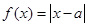 .
.
(1)当 时,解不等式
时,解不等式 ;
;
(2)若 的解集为
的解集为 ,
, ,求证:
,求证: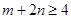 .
.
已知极坐标系的极点在直角坐标系的原点处,极轴与x轴的正半轴重合,直线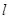 的极坐标方程为
的极坐标方程为 ,曲线C的参数方程是
,曲线C的参数方程是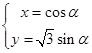 (
(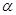 是参数).
是参数).
(1)求直线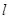 的直角坐标方程及曲线C的普通方程;
的直角坐标方程及曲线C的普通方程;
(2)求曲线C上的点到直线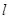 的最大距离.
的最大距离.
如图, 是
是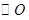 的一条切线,切点为B,ADE,CFD和CGE都是
的一条切线,切点为B,ADE,CFD和CGE都是 的割线,
的割线, .
.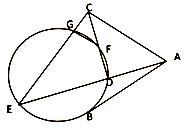
(1)证明: ;
;
(2)证明:
已知函数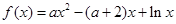 ,其中
,其中 .
.
(1)当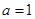 时,求曲线
时,求曲线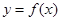 的点
的点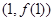 处的切线方程;
处的切线方程;
(2)当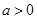 时,若
时,若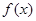 在区间
在区间 上的最小值为-2,求
上的最小值为-2,求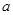 的取值范围;
的取值范围;
(3)若 ,且
,且 恒成立,求
恒成立,求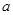 的取值范围.
的取值范围.
已知抛物线 的焦点为
的焦点为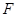 ,
, 为
为 上异于原点的任意一点,过点
上异于原点的任意一点,过点 的直线
的直线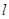 交
交 于另一点
于另一点 ,交
,交 轴的正半轴于点
轴的正半轴于点 ,且有
,且有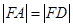 ,当点
,当点 的横坐标为3时,
的横坐标为3时, 为正三角形.
为正三角形.
(1)求C的方程;
(2)若直线 ,且
,且 和C有且只有一个公共点E.
和C有且只有一个公共点E.
①证明直线AE过定点,并求出定点坐标;
②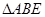 的面积是否存在最小值?若存在,请求出最小值;若不存在,请说明理由.
的面积是否存在最小值?若存在,请求出最小值;若不存在,请说明理由.