已知函数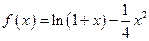 ;
;
(1)求函数在点 处的切线方程;
处的切线方程;
(2)求函数在 上的最大值和最小值.
上的最大值和最小值.
在△ABC中,a,b,c分别为角A,B,C的对边,设 f(x)=a2x2-(a2-b2)x-4c2.
(1)若 f(1)=0,且B-C= ,求角C;
,求角C;
(2)若 f(2)=0,求角C的取值范围.
如图,设 是单位圆和
是单位圆和 轴正半轴的交点,
轴正半轴的交点, 是单位圆上
是单位圆上 的两点,
的两点, 是坐标原点,
是坐标原点, ,
, .
.
(1)若 ,求
,求 的值;
的值;
(2)设函数 ,求
,求 的值域.
的值域.
已知向量 ,
,
(1)当 时,求
时,求 的取值集合;(2)求函数
的取值集合;(2)求函数 的单调递增区间
的单调递增区间
已知函数 ,
,  .
.
(Ⅰ)求函数 的最大值和最小值;
的最大值和最小值;
(Ⅱ)设函数 在
在 上的图象与
上的图象与 轴的交点从左到右分别为M、
轴的交点从左到右分别为M、 N,图象的最高点为P,求
N,图象的最高点为P,求 与
与 的夹角的余弦.
的夹角的余弦.
已知: 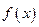 是定义在区间
是定义在区间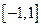 上的奇函数,且
上的奇函数,且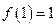 .若对于任意的
.若对于任意的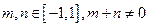 时,都有
时,都有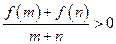 .
.
(1)解不等式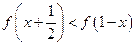 .
.
(2)若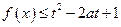 对所有
对所有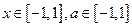 恒成立,求实数
恒成立,求实数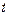 的取值范围
的取值范围