(本小题满分12分)已知双曲线的焦点在y轴上,两顶点间的 距离为4,渐近线方程为
距离为4,渐近线方程为
y=±2x.
(Ⅰ)求双曲线的标准方程;
(Ⅱ)设(Ⅰ)中双曲线的焦点F1,F2关于直线y=x的对称点分别为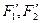 ,求以
,求以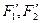
 为焦点,且过点P(0,2)的椭圆方程.
为焦点,且过点P(0,2)的椭圆方程.
(本小题满分12分)(如图,某海滨浴场的岸边可近似地看成直线,位于岸边A处的救生员发现海中B处有人求救,救生员没有直接从A处游向B处,而是沿岸边自A跑到距离B最近的D处,然后游向B处,若救生员在岸边的行进速度为6米/秒,在海中的行进速度为2米/秒,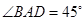 。
。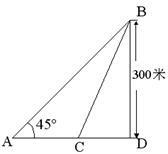
(1)分析救生员的选择是否正确;
(2)在AD上找一点C,使救生员从A到B的时间为最短,并求出最短时间。
(本小题满分12分)在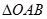 中,已知点
中,已知点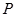 为线段
为线段 上的一点,且
上的一点,且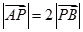 .
.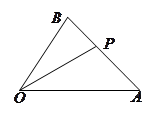
(1)试用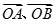 表示
表示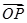 ;
;
(2)若 ,且
,且 ,求
,求 的值.
的值.
(本小题12分)已知sin(2α-β)=  ,sinβ=" -"
,sinβ=" -" 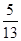 ,且α∈(
,且α∈(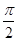 ,π),β∈(-
,π),β∈(-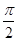 ,0),求sinα的值.
,0),求sinα的值.
已知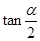 =2,求值:
=2,求值:
(1) ;
;
(2)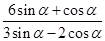 .
.
如图,分别以菱形BCED的对角线BE、CD所在直线为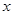 轴、
轴、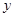 轴建立平面直角坐标系,抛物线
轴建立平面直角坐标系,抛物线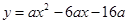 (
(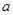 <0)过B、C两点,与
<0)过B、C两点,与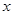 轴的负半轴交于点A,且∠ACB=90°.点P是
轴的负半轴交于点A,且∠ACB=90°.点P是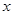 轴上一动点,设点P的坐标为(
轴上一动点,设点P的坐标为(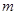 ,0),过点P作直线
,0),过点P作直线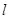 垂直于
垂直于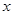 轴,交抛物线于点Q.
轴,交抛物线于点Q.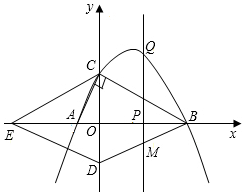
(1)求点A、B、C的坐标及抛物线的解析式;
(2)当点P在线段OB上运动时,直线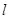 交BD于点M,试探究:
交BD于点M,试探究:
①求MQ的大小;(用含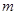 的化简式子表示)
的化简式子表示)
②当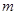 为何值时,四边形CQBM的面积取得最大值,并求出这个最大值.
为何值时,四边形CQBM的面积取得最大值,并求出这个最大值.
(3)当点P在线段EB上运动时,是否存在点 Q,使△BDQ为直角三角形,若存在,请直接写出点Q的坐标;若不存在,请说明理由