在直角坐标系 中,点P到两点
中,点P到两点 ,
, 的距离之和等于4,设点P的轨迹为
的距离之和等于4,设点P的轨迹为 ,直线
,直线 与轨迹C交于A,B两点.
与轨迹C交于A,B两点.
(Ⅰ)写出轨迹C的方程;(Ⅱ)若

 ,求k的值;
,求k的值;
(Ⅲ)若点A在第一象限,证明:当k>0时,恒有| |>|
|>| |
|
设数列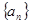 的前项n和为
的前项n和为 ,若对于任意的正整数n都有
,若对于任意的正整数n都有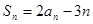 .
.
(1)求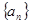 的通项公式。
的通项公式。
(2)求数列 的前n项和.
的前n项和.
给定两个命题, 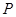 :对任意实数
:对任意实数 都有
都有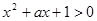 恒成立;
恒成立;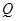 :关于
:关于 的方程
的方程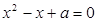 有实数根.如果
有实数根.如果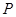 ∨
∨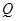 为真命题,
为真命题,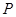 ∧
∧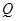 为假命题,求实数
为假命题,求实数 的取值范围.
的取值范围.
某工厂家具车间造A、B型两类桌子,每张桌子需木工和漆工两道工序完成.已知木工做一张A、B型桌子分别需要1小时和2小时,漆工油漆一张A、B型桌子分别需要3小时和1小时;又知木工、漆工每天工作分别不得超过8小时和9小时,而工厂造一张A、B型桌子分别获利润2千元和3千元,试问工厂每天应生产A、B型桌子各多少张,才能获得利润最大?
如果方程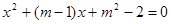 的两个实根一个小于‒1,另一个大于0,求实数m的取值范围
的两个实根一个小于‒1,另一个大于0,求实数m的取值范围