(本小题满分12分)已知函数
(I)求函数 的单调区间; (II)当
的单调区间; (II)当 在区间[—1,2]上是单调函数,求a的取值范围。
在区间[—1,2]上是单调函数,求a的取值范围。
(本小题满分10分)
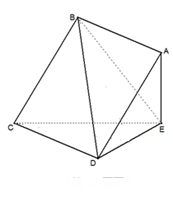
如图,平面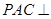 平面
平面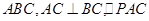 为等边三角形,
为等边三角形, 分别是线段
分别是线段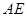 ,
, 上的动点,且满足:
上的动点,且满足: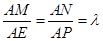
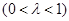 .
.
(Ⅰ)求证: ∥平面
∥平面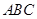 ;
;
(Ⅱ)当 时,求平面ABC与平面MNC所成的锐二面角的大小.
时,求平面ABC与平面MNC所成的锐二面角的大小.
(本小题满分10分)如图,在四棱锥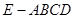 中,底面
中,底面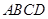 为正方形,
为正方形, 平面
平面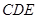 ,已知
,已知 .
.
(Ⅰ)求证:平面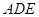
 平面
平面 ;
;
(Ⅱ)求直线 与平面
与平面 所成角的正弦值.
所成角的正弦值.
如图,直线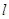 过点
过点 ,夹在两已知直线
,夹在两已知直线 和
和 之间的线段
之间的线段 恰被点
恰被点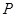 平分.
平分.
(Ⅰ)求直线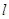 的方程;
的方程;
(Ⅱ)设点 ,且
,且 ,求:
,求: 的面积.
的面积.
已知 ,
,
(1)若f(x)的最小值记为h(a),求h(a)的解析式.
(2)是否存在实数m,n同时满足以下条件:① ;②当h(a)的定义域为[n,m]时,值域为[n2,m2];若存在,求出m,n的值;若不存在,说明理由.
;②当h(a)的定义域为[n,m]时,值域为[n2,m2];若存在,求出m,n的值;若不存在,说明理由.
已知函数 ,其中常数a,b为实数.
,其中常数a,b为实数.
(1)当a>0,b>0时,判断并证明函数 的单调性;
的单调性;
(2)当ab<0时,求 时的
时的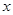 的取值范围.
的取值范围.