(本小题满分10分)
如图,平面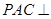 平面
平面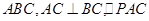 为等边三角形,
为等边三角形, 分别是线段
分别是线段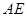 ,
, 上的动点,且满足:
上的动点,且满足: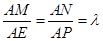
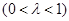 .
.
(Ⅰ)求证: ∥平面
∥平面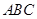 ;
;
(Ⅱ)当 时,求平面ABC与平面MNC所成的锐二面角的大小.
时,求平面ABC与平面MNC所成的锐二面角的大小.
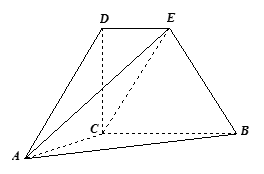
(本小题满分12分)如图,四边形 为直角梯形,
为直角梯形,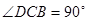 ,
, ,
, ,又
,又 ,
,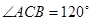 ,
, ,直线
,直线 与直线
与直线 所成角为
所成角为 .
.
(Ⅰ)求证:平面 平面
平面 ;
;
(Ⅱ)求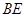 与平面
与平面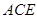 所成角的正弦值.
所成角的正弦值.
(本小题满分12分)
如图,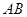 是底部
是底部 不可到达的一个塔型建筑物,
不可到达的一个塔型建筑物, 为塔的最高点.现需在对岸测出塔高
为塔的最高点.现需在对岸测出塔高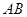 ,甲、乙两同学各提出了一种测量方法,甲同学的方法是:选与塔底
,甲、乙两同学各提出了一种测量方法,甲同学的方法是:选与塔底 在同一水平面内的一条基线
在同一水平面内的一条基线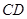 ,使
,使 三点不在同一条直线上,测出
三点不在同一条直线上,测出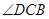 及
及 的大小(分别用
的大小(分别用 表示测得的数据)以及
表示测得的数据)以及 间的距离(用
间的距离(用 表示测得的数据),另外需在点
表示测得的数据),另外需在点 测得塔顶
测得塔顶 的仰角(用
的仰角(用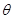 表示测量的数据),就可以求得塔高
表示测量的数据),就可以求得塔高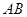 .乙同学的方法是:选一条水平基线
.乙同学的方法是:选一条水平基线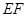 ,使
,使 三点在同一条直线上.在
三点在同一条直线上.在 处分别测得塔顶
处分别测得塔顶 的仰角(分别用
的仰角(分别用 表示测得的数据)以及
表示测得的数据)以及 间的距离(用
间的距离(用 表示测得的数据),就可以求得塔高
表示测得的数据),就可以求得塔高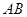 .
.
请从甲或乙的想法中选出一种测量方法,写出你的选择并按如下要求完成测量计算:①画出测量示意图;②用所叙述的相应字母表示测量数据,画图时 按顺时针方向标注,
按顺时针方向标注, 按从左到右的方向标注;③求塔高
按从左到右的方向标注;③求塔高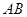 .
.
(本小题满分10分)选修4—5:不等式选讲
已知关于x的不等式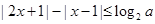 (其中
(其中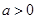 ).
).
(1)当a=4时,求不等式的解集;
(2)若不等式有解,求实数a的取值范围
(本小题满分10分)选修4—4:坐标系与参数方程
在极坐标系中,曲线 ,过点A(5,α)(α为锐角且
,过点A(5,α)(α为锐角且 )作平行于
)作平行于 的直线
的直线 ,且
,且 与曲线L分别交于B,C两点.
与曲线L分别交于B,C两点.
(1)以极点为原点,极轴为x轴的正半轴,取与极坐标相同单位长度,建立平面直角坐标系,写出曲线L和直线 的普通方程;
的普通方程;
(2)求|BC|的长
(本小题满分10分)选修41:几何证明选讲
如图, 相交于A、B两点,AB是
相交于A、B两点,AB是 的直径,过A点作
的直径,过A点作 的切线交
的切线交 于点E,并与BO1的延长线交于点P,PB分别与
于点E,并与BO1的延长线交于点P,PB分别与 、
、 交于C,D两点.
交于C,D两点.
求证:(1)PA·PD=PE·PC;
(2)AD=AE