在某校教师趣味投篮比赛中,比赛规则是: 每场投6个球,至少投进4个球且最后2个球都投进者获奖;否则不获奖. 已知教师甲投进每个球的概率都是 .
.
(1)记教师甲在每场的6次投球中投进球的个数为X,求X的分布列及数学期望;
(2)求教师甲在一场比赛中获奖的概率;
(3)已知教师乙在某场比赛中,6个球中恰好投进了4个球,求教师乙在这场比赛中获奖的概率;教师乙在这场比赛中获奖的概率与教师甲在一场比赛中获奖的概率相等吗?
(本小题满分13分)某单位有三辆汽车参加某种事故保险,单位年初向保险公司
缴纳每辆900元的保险金.对在一年内发生此种事故的每辆汽车,单位获9000元
的赔偿(假设每辆车最多只赔偿一次)。设这三辆车在一年内发生此种事故的概率
分别为 且各车是否发生事故相互独立,求一年内该单位在此保险中:
且各车是否发生事故相互独立,求一年内该单位在此保险中:
(1)获赔的概率;(4分)
(2)获赔金额 的分别列与期望。(9分)
的分别列与期望。(9分)
(本小题满分12分)如图,中心在原点O的椭圆的右焦点为F(3,0),
右准线l的方程为:x = 12。
(1)求椭圆的方程;(4分)
(2)在椭圆上任取三个不同点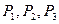 ,使
,使 ,
,
证明: 为定值,并求此定值。(8分)
为定值,并求此定值。(8分)
|
(本小题满分12分)已知各项均为正数的数列{ }的前n项和满足
}的前n项和满足 ,且
,且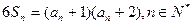
(1)求{ }的通项公式;(5分)
}的通项公式;(5分)
(2)设数列{ }满足
}满足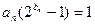 ,并记
,并记 为{
为{ }的前n项和,
}的前n项和,
求证: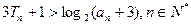 . (7分)
. (7分)
(本小题满分13分)已知函数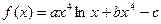 (x>0)在x = 1处
(x>0)在x = 1处
取得极值–3–c,其中a,b,c为常数。
(1)试确定a,b的值;(6分)
(2)讨论函数f(x)的单调区间;(4分)
(3)若对任意x>0,不等式 恒成立,求c的取值范围。(3分)
恒成立,求c的取值范围。(3分)
(本小题满分13分)设f (x) = 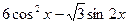
(1)求f(x)的最大值及最小正周期; (9分)
(2)若锐角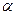 满足
满足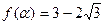 ,求tan
,求tan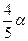 的值。(4分)
的值。(4分)