.(本小题满分12分)数列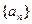 的前
的前 项和记为
项和记为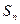 ,
,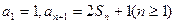
(1) 求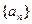 的通项公式;
的通项公式;
(2) 等差数列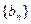 的各项为正,其前
的各项为正,其前 项和为
项和为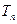 ,且
,且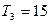 ,
,
a,b,c是△ABC的三边长,关于x的方程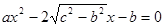 (a>c>b)的两根之差的平方等于4,△ABC的面积S=10
(a>c>b)的两根之差的平方等于4,△ABC的面积S=10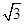 ,c=7.
,c=7.
(1)求角C;
(2)求a、 的值.
的值.
已知全集U=R,集合A={x|x2+(a-1)x-a>0},
B={x|(x+a)(x+b)>0(a≠b)},M={x|x2-2x-3≤0}.
(1)若∁UB=M,求a,b的值;
(2)若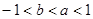 ,求A∩B;
,求A∩B;
(3)若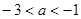 ,且
,且 ∁UA,求实数
∁UA,求实数 的取值范围.
的取值范围.
某单位用木料制作如图所示的框架, 框架的下部是边长分别为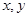 (单位:m)的矩形,上部是等腰直角三角形要求框架围成的总面积8cm2问
(单位:m)的矩形,上部是等腰直角三角形要求框架围成的总面积8cm2问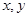 分别为多少(保留根号) 时用料最省?
分别为多少(保留根号) 时用料最省?
已知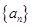 是首项为19,公差为-2的等差数列,
是首项为19,公差为-2的等差数列, 为
为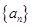 的前
的前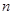 项和.
项和.
(1)求通项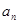 及
及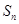 ;
;
(2)设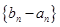 是首项为1,公比为3的等比数列,求数列
是首项为1,公比为3的等比数列,求数列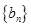 的通项公式及其前
的通项公式及其前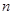 项和
项和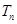 .
.
(本小题满分14分)
(1) 证明:当 时,不等式
时,不等式 成立;
成立;
(2) 要使上述不等式 成立,能否将条件“
成立,能否将条件“ ”适当放宽?若能,请放宽条件并简述理由;若不能,也请说明理由;
”适当放宽?若能,请放宽条件并简述理由;若不能,也请说明理由;
(3)请你根据⑴、⑵的证明,试写出一个类似的更为一般的结论,且给予证明.