(本小题共14分)
已知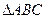 的边
的边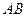 边所在直线的方程为
边所在直线的方程为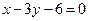
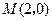 满足
满足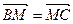 , 点
, 点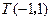 在AC边所在直线上
在AC边所在直线上
且满足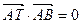 .
.
(I)求AC边所在直线的方程;
(II)求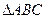 外接圆的方程;
外接圆的方程;
(III)若动圆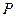 过点
过点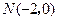 ,且与
,且与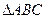 的外接圆外切,求动圆
的外接圆外切,求动圆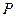 的圆心的轨迹方程.请注意下面两题用到求和符号:
的圆心的轨迹方程.请注意下面两题用到求和符号:
f(k)+f(k+1)+f(k+2)+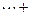 f(n)=
f(n)=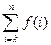 ,其中k, n为正整数且k
,其中k, n为正整数且k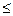 n
n
( 10分)已知双曲线 的左、右焦点分别为
的左、右焦点分别为 ,
, ,过点
,过点 的动直线与双曲线相交于
的动直线与双曲线相交于 两点.
两点.
(I)若动点 满足
满足 (其中
(其中 为坐标原点),求点
为坐标原点),求点 的轨迹方程;
的轨迹方程;
(II)在 轴上是否存在定点
轴上是否存在定点 ,使
,使 ·
· 为常数?若存在,求出点
为常数?若存在,求出点 的坐标;
的坐标;
若不存在,请说明理由.
已知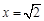 是函数
是函数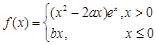 的极值点.当
的极值点.当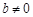 时,讨论函数
时,讨论函数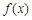 的单调性;
的单调性;
( 10分)如图,四面体ABCD中,O、E分别是BD、BC的中点,CA=CB=CD=BD=2,AB=AD=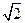 。
。
1)求证:AO 平面BCD;
平面BCD;
2)求异面直线AB与CD所成角的余弦值;
3)求点E到平面ACD的距离。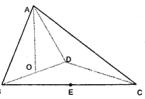
( 9分)如图,过椭圆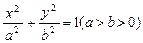 的左焦点F任作一条与两坐标轴都不垂直的弦AB,若点M在x轴上,且使得MF为△AMB的一条内角平分线,则称点M为该椭圆的“左特征点”.求椭圆
的左焦点F任作一条与两坐标轴都不垂直的弦AB,若点M在x轴上,且使得MF为△AMB的一条内角平分线,则称点M为该椭圆的“左特征点”.求椭圆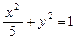 的“左特征点”M的坐标;
的“左特征点”M的坐标;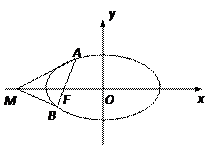
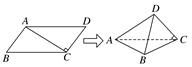
(8分)在平行四边形ABCD中,AB=AC=1,∠ACD=90°,将它沿对角线AC折起,使AB和CD成60°角(见下图).求B、D间的距离