(本小题满分14分)
设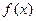 是定义在
是定义在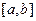 上的函数,用分点
上的函数,用分点
将区间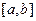 任意划分成
任意划分成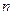 个小区间,如果存在一个常数
个小区间,如果存在一个常数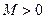 ,使得和式
,使得和式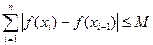 (
(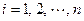 )恒成立,则称
)恒成立,则称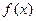 为
为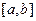 上的有界变差函数.
上的有界变差函数.
(1)函数 在
在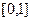 上是否为有界变差函数?请说明理由;
上是否为有界变差函数?请说明理由;
(2)设函数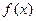 是
是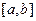 上的单调递减函数,证明:
上的单调递减函数,证明: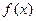 为
为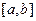 上的有界变差函数;
上的有界变差函数;
(3)若定义在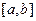 上的函数
上的函数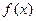 满足:存在常数
满足:存在常数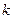 ,使得对于任意的
,使得对于任意的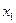 、
、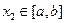 时,
时,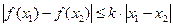 .证明:
.证明: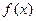 为
为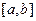 上的有界变差函数.
上的有界变差函数.
(本小题满分10分)已知圆C的极坐标方程为 =2,以极点为原点,极轴为x轴的正半轴建立平面直角坐标系,若直线
=2,以极点为原点,极轴为x轴的正半轴建立平面直角坐标系,若直线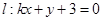 与圆C相切.
与圆C相切.
求(1)圆C的直角坐标方程;
(2)实数k的值.
(本小题满分10分)已知函数f(x)=ln(2x-e), 点P(e,f(e))为函数的图像上一点
(1)求导函数 的解析式;
的解析式;
(2)求f(x)=ln(2x-e)在点P(e,f(e))处的切线的方程.
(本小题满分16分)设函数f(x)=xsinx(x∈R),
(Ⅰ)证明f(x+2kπ)-f(x)=2kπsinx,其中k为整数;
(Ⅱ)设x0为f(x)的一个极值点,证明  ;
;
(提示 )
)
(Ⅲ)设f(x)在(0,+∞)内的全部极值点按从小到大的顺序排列a1,a2, ,an, ,证明 .
.
(本小题满分16分)已知函数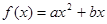 的图像过点
的图像过点 ,且在
,且在 处的切线的斜率为
处的切线的斜率为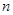 ,(
,(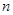 为正整数)
为正整数)
(Ⅰ)求函数 的解析式;
的解析式;
(Ⅱ)若数列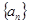 满足:
满足: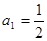 ,
, ,令
,令 ,求数列
,求数列 的通项公式;
的通项公式;
(Ⅲ)对于(Ⅱ)中的数列 ,令
,令 ,求数列
,求数列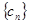 的前
的前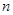 项的和
项的和 .
.
(本小题满分16分)已知奇函数 的定义域为
的定义域为 ,当
,当 时,
时, .
.
(1)求函数 在
在 上的值域;
上的值域;
(2)若 ,y=
,y= 的最小值为
的最小值为 ,求实数
,求实数 的值.
的值.