.(本小题满分14分)
已知函数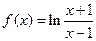
(Ⅰ)求函数的定 义域,并证明
义域,并证明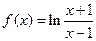 在定义域上是奇函数;
在定义域上是奇函数;
(Ⅱ)若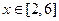
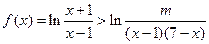 恒成立,求实数
恒成立,求实数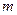 的取值范围;
的取值范围;
(Ⅲ)当 时,试比较
时,试比较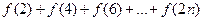 与
与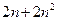 的大小关系
的大小关系
(本小题满分12分)
某电视台拟举行“团队共享”冲关比赛,其规则如下:比赛共设有“常识关”和“创新关”两关,每个团队共两人,每人各冲一关,“常识关”中有2道不同必答题,“创新关”中有3道不同必答题;如果“常识关”中的2道题都答对,则冲“常识关”成功且该团队获得单项奖励900元,否则无奖励;如果“创新关”中的3道题至少有2道题答对,则冲“创新关”成功且该团队获得单项奖励1800元,否则无奖励.现某团队中甲 冲击“常识关”,乙冲击“创新关”,已知甲回答“常识关”中每道题正确的概率都为
冲击“常识关”,乙冲击“创新关”,已知甲回答“常识关”中每道题正确的概率都为 ,乙回答“创新关”中每道题正确的概率都为
,乙回答“创新关”中每道题正确的概率都为 ,且两关之间互不影响,每道题回答正确与否相互独立.
,且两关之间互不影响,每道题回答正确与否相互独立.
(I)求此冲关团队在这5道必答题中只有2道回答正确且没有获得任何奖励的概率;
(Ⅱ)记此冲关团队获得的奖励总金额为随机变量 ,求
,求 的分布列和数学期望
的分布列和数学期望 .
.
(本小题满分12分)
如图,边长为1的正三角形 所在平面与直角梯形
所在平面与直角梯形 所在平面垂直,且
所在平面垂直,且 ,
, ,
, ,
, ,
, 、
、 分别是线段
分别是线段 、
、 的中点.
的中点.
(I)求证:平面 平面
平面 ;
;
(Ⅱ)求二面角 的大小.
的大小.
三、解答题:本大题共6小题,共74分.解答应写出文字说明,证明过程或演算步骤.
(17)(本小题满分12分)
已知函数 .
.
(I)求函数 的最小正周期;
的最小正周期;
(Ⅱ)当 时,函数
时,函数 的最小值为
的最小值为 ,求实数
,求实数 的值.
的值.
(附加题)若角
 的终边过
的终边过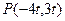
 ,求
,求 的值。
的值。
、一扇形的周长为20,则扇形的半径和圆心角各取什么值时,才能使扇形面积最大?