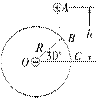a（1）在《验证机械能守恒定律》的实验中，打点计时器所用电源为50Hz，当地重力加速度的值为9.80m/s2，测得所用重物的质量为1.00kg，甲、乙、丙三学生分别用同一装置打出三条纸带，量出各纸带上第1、2两点间的距离分别为0.18cm、0.19cm、0.25cm，从纸带中可看出 学生在操作上肯定有错误，可能的原因是 。
（2）在一次实验中，质量m=1kg的重物自由下落，在纸带上打出一系列的点，如图所示（相邻计数点时间间隔为0.
02s），单位cm，那么纸带的 端与重物相连； 打点计时器打下计数点B时，物体的速度vB=" " ； 从起点O到打下计数点B的过程中重力势能减少量△EP=" " ；此过程中物体动能的增加量△EK=" " （g=9.80m/s2）； 通过计算，数值上△EP △EK（填“>”、“=”、或“<”），这是因为 
；实验的结论是 。
b.在探究小车的加速度a与小车质量M和小车受到的外力F的关系时，
⑴探究加速度和力的关系的实验数据描绘出的a-F图象如图所示，下列说法正确的是
A．三条倾斜的直线所对应的小车的质量相等 |
B．三条 倾斜的直线所对应的小车的质量不同 |
| C．直线1所对应的小车的质量最大 |
| D．直线3所对应的小车的质量最大 |
⑵由于没有始终满足小车的质量
远大于钩码的质量m的关系，结果得到的图象应是下图中的（ ）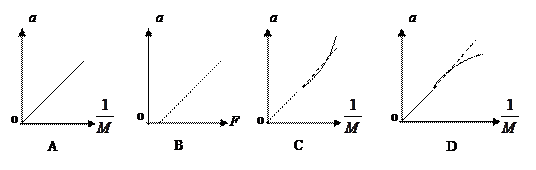
一辆汽车从原点O由静止出发沿x轴做直线运动，为研究汽车运动的规律而记录下它在不同时刻的位置和速度，见下表所示．试求：
| 时刻t/s |
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
| 位置坐标x/m |
0 |
0.5 |
2 |
4.5 |
8 |
12 |
16 |
20 |
（1）试判断前4 s内汽车做的是什么运动？ 若为匀速直线运动，求出前4 s内的速度；若为变速直线运动，求出前4 s内的加速度；
（2）汽车在3.5 s末的速度和5.5s末的速度．
甲车以加速度3m/s2由静止开始作匀加速直线运动，乙车落后2s钟在同一地点由静止开始，以加速度49/12m/s2作匀加速直线运动，两车的运动方向相同。
求： 乙车出发后经多长时间可追上甲车？此时它们离开出发点多远？
如图所示，水平光滑地面上停放着一辆小车，左侧靠在竖直墙壁上，小车的四分之一圆弧轨道 AB是光滑的，在最低点 B与水平轨道 BC相切， BC的长度是圆弧半径的4倍，整个轨道处于同一竖直平面内．可视为质点的物块从 A点正上方某处无初速下落而切入小车圆弧轨道滑动，然后沿水平轨道 BC滑行至轨道末端 C处恰好没有滑出．已知物块到达圆弧轨道最低点 B时对轨道的压力是物块重力的5 倍，小车的质量是物块的3倍，不考虑空气阻力和物块落入圆弧轨道时的能量损失．求：
| 1． |
物块开始下落的位置距A的高度是圆弧半径的几倍； |
| 2． |
物块与水平轨道 BC间的动摩擦因数 μ. |
如图所示，分别在A、B两点放置等量同种点电荷1、2，电量均为Q．记AB的中点为O，OA=OB=a，在AB的垂直平分线上有一点C，OC=x．试求C点的场强．
如图所示，在O点放置一个正电荷．在过O点的竖直平面内的A点，自由释放一个带正电的小球，小球的质量为m、电荷量为q.小球落下的轨迹如图中虚线所示，它与以O为圆心、R为半径的圆(图中实线表示)相交于B、C两点，O、C在同一水平线上，∠BOC＝30°，A距离OC的竖直高度为h.若小球通过B点的速度为v，试求UCA=？