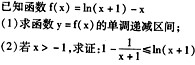
(12)设焦点在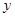 轴上的双曲线渐近线方程为
轴上的双曲线渐近线方程为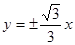 ,且离心率为2,已知点A(
,且离心率为2,已知点A(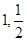 )
)
(1)求双曲线的标准方程;
(2)过点A的直线L交双曲线于M,N两点,点A为线段MN的中点,求直线L方程。
函数 ,过曲线
,过曲线 上的点
上的点 的切线斜率为3.
的切线斜率为3.
(1)若 在
在 时有极值,求f (x)的表达式;
时有极值,求f (x)的表达式;
(2)在(1)的条件下,求 在
在 上最大值;
上最大值;
设p: 实数 ,q:实数
,q:实数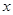 满足
满足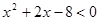 ,
,
且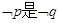 的必要不充分条件,求
的必要不充分条件,求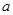 的取值范围。
的取值范围。
已知 点在以坐标轴为对称轴的椭圆上,点
点在以坐标轴为对称轴的椭圆上,点 到两焦点的距离分别为4和2,过
到两焦点的距离分别为4和2,过 点作焦点所在轴的垂线,它恰好过椭圆的一个焦点,求椭圆方程.
点作焦点所在轴的垂线,它恰好过椭圆的一个焦点,求椭圆方程.
如图,已知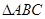 的三边长分别为
的三边长分别为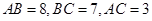 ,以点
,以点 为圆心,
为圆心,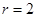 为半径作一个圆.
为半径作一个圆.
(1) 求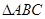 的面积;
的面积;
(2)设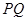 为
为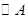 的任意一条直径,记
的任意一条直径,记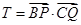 ,求
,求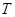 的最大值和最小值,并说明当
的最大值和最小值,并说明当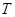 取最大值和最小值时,
取最大值和最小值时,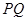 的位置特征是什么?
的位置特征是什么?