(本小题满分10分)
如图,矩形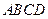 的两条对角线相交于点
的两条对角线相交于点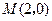 ,
, 边所在直线的方程为
边所在直线的方程为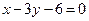 , 点
, 点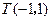 在
在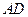 边所在直线上.
边所在直线上.
(1)求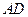 边所在直线的方程;
边所在直线的方程;
(2)求矩形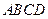 外接圆的方程
外接圆的方程 ;
;
数列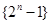 的前
的前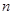 项组成集合
项组成集合 ,从集合
,从集合 中任取
中任取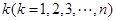 个数,其所有可能的
个数,其所有可能的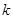 个数的乘积的和为
个数的乘积的和为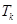 (若只取一个数,规定乘积为此数本身),记
(若只取一个数,规定乘积为此数本身),记 .例如:当
.例如:当 时,
时, ,
, ,
,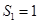 ;当
;当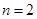 时,
时, ,
, ,
,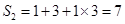 .
.
(Ⅰ)求 ;
;
(Ⅱ)猜想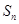 ,并用数学归纳法证明.
,并用数学归纳法证明.
如图(1),等腰直角三角形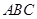 的底边
的底边 ,点
,点 在线段
在线段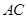 上,
上,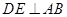 于
于 ,现将
,现将 沿
沿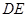 折起到
折起到 的位置(如图(2)).
的位置(如图(2)).
(Ⅰ)求证: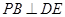 ;
;
(Ⅱ)若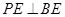 ,直线
,直线 与平面
与平面 所成的角为
所成的角为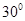 ,求
,求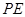 长.
长.
某舞蹈小组有2名男生和3名女生.现从中任选2人参加表演,记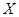 为选取女生的人数,求X的分布列及数学期望.
为选取女生的人数,求X的分布列及数学期望.
求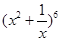 展开式中的常数项.
展开式中的常数项.
已知各项均为正数的两个无穷数列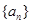 、
、 满足
满足 .
.
(Ⅰ)当数列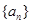 是常数列(各项都相等的数列),且
是常数列(各项都相等的数列),且 时,求数列
时,求数列 的通项公式;
的通项公式;
(Ⅱ)设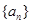 、
、 都是公差不为0的等差数列,求证:数列
都是公差不为0的等差数列,求证:数列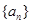 有无穷多个,而数列
有无穷多个,而数列 惟一确定;
惟一确定;
(Ⅲ)设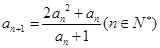 ,
,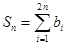 ,求证:
,求证: .
.