(本小题满分13分)
给定椭圆 >
> >0
>0 ,称圆心在原点
,称圆心在原点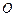 ,半径为
,半径为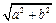 的圆是椭圆
的圆是椭圆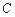 的“准圆”
的“准圆” 。若椭圆
。若椭圆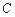 的一个焦点为
的一个焦点为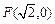 ,其短轴上的一个端点到
,其短轴上的一个端点到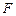 的距离为
的距离为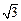 。
。
(1)求椭圆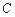 的方程和其“准圆”方程;
的方程和其“准圆”方程;
(2)点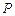 是椭圆
是椭圆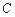 的“准圆”上的一个动点,过点
的“准圆”上的一个动点,过点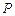 作直线
作直线 ,使得
,使得 与椭圆
与椭圆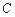 都只有一个交点。求证:
都只有一个交点。求证: ⊥
⊥ .
.
设函数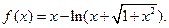
(Ⅰ) 讨论函数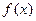 的单调性;
的单调性;
(Ⅱ)若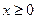 时,恒有
时,恒有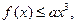 试求实数
试求实数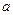 的取值范围;
的取值范围;
(Ⅲ)令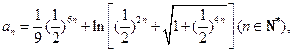
试证明: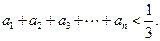
如图,已知直线l与抛物线 相切于点P(2,1),且与x轴交于点A,O为坐标原点,定点B的坐标为(2,0).
相切于点P(2,1),且与x轴交于点A,O为坐标原点,定点B的坐标为(2,0). 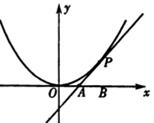
(I) 若动点M满足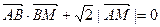 ,求点M的轨迹C;
,求点M的轨迹C;
(II)若过点B的直线l′(斜率不等于零)与(I)中的轨迹C交于不同的两点E、F(E在B、F之间),试求△OBE与△OBF面积之比的取值范围
如图,在四棱锥P-ABCD中,底面ABCD为直角梯形,AD//BC,∠ADC=90°,平面PAD⊥底面ABCD,Q为AD的中点,M为PC上一点,PA=PD=2,BC=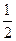 AD=1,CD=
AD=1,CD=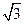 .
.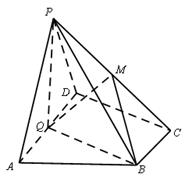
(Ⅰ)求证:平面PQB⊥平面PAD;
(Ⅱ)若二面角M-BQ-C为30°,设PM=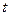 MC,试确定
MC,试确定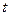 的值.
的值.
在某校教师趣味投篮比赛中,比赛规则是: 每场投6个球,至少投进4个球且最后2个球都投进者获奖;否则不获奖. 已知教师甲投进每个球的概率都是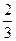 .
.
(Ⅰ)记教师甲在每场的6次投球中投进球的个数为X,求X的分布列及数学期望;
(Ⅱ)求教师甲在一场比赛中获奖的概率;
(Ⅲ)已知教师乙在某场比赛中,6个球中恰好投进了4个球,求教师乙在这场比赛中获奖的概率;教师乙在这场比赛中获奖的概率与教师甲在一场比赛中获奖的概率相等吗?
已知各项都不相等的等差数列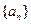 的前6项和为60,且
的前6项和为60,且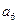 为
为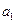 和
和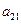 的等比中项.
的等比中项.
( I )求数列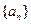 的通项公式;
的通项公式;
(II) 若数列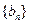 满足
满足 ,且
,且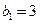 ,求数列
,求数列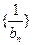 的前
的前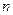 项和
项和 .
.