在某校教师趣味投篮比赛中,比赛规则是: 每场投6个球,至少投进4个球且最后2个球都投进者获奖;否则不获奖. 已知教师甲投进每个球的概率都是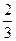 .
.
(Ⅰ)记教师甲在每场的6次投球中投进球的个数为X,求X的分布列及数学期望;
(Ⅱ)求教师甲在一场比赛中获奖的概率;
(Ⅲ)已知教师乙在某场比赛中,6个球中恰好投进了4个球,求教师乙在这场比赛中获奖的概率;教师乙在这场比赛中获奖的概率与教师甲在一场比赛中获奖的概率相等吗?
如图,在四棱锥P-ABCD中,PD⊥面ABCD,AD∥BC,CD=13,AB=12,BC=10,AD= BC. 点E、F分别是棱PB、边CD的中点.
BC. 点E、F分别是棱PB、边CD的中点.
(1)求证:AB⊥面PAD;
(2)求证:EF∥面PAD.
如图,摩天轮的半径为50 m,点O距地面的高度为60 m,摩天轮做匀速转动,每3 min转一圈,摩天轮上点P的起始位置在最低点处.
(1)试确定在时刻t(min)时点P距离地面的高度;
(2)在摩天轮转动的一圈内,有多长时间点P距离地面超过85 m?
已知函数 .
.
(1)求 的单调区间;
的单调区间;
(2)设 ,若对任意
,若对任意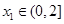 ,均存在
,均存在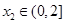 ,使得
,使得 <
<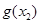 ,求
,求 的取值范围.
的取值范围.
已知过点 的动直线
的动直线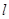 与抛物线
与抛物线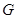 :
: 相交于
相交于 两点.当直线
两点.当直线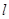 的斜率是
的斜率是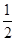 时,
时,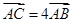 .
.
(1)求抛物线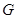 的方程;
的方程;
(2)设线段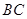 的中垂线在
的中垂线在 轴上的截距为
轴上的截距为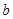 ,求
,求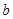 的取值范围.
的取值范围.
如图,在四棱锥 中,底面
中,底面 是矩形,
是矩形,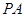 ⊥平面
⊥平面 ,
, ,
, ,
, 分别是
分别是 的中点.
的中点.
(1)证明: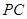 ⊥平面
⊥平面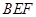 ;
;
(2)求平面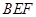 与平面
与平面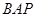 夹角的大小.
夹角的大小. 