（本小题满分12分）如图，已知抛物线
:
的准线为直线
，过点
的动直线
交抛物线于
,
两点．
（Ⅰ）求抛物线的方程；
（Ⅱ）若以线段
为直径的圆恒过抛物线上的某定点
（异于
两点），求
的值和点的坐标．
已知函数f(x)＝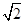
cos
，x∈R
(1)求f
的值；
(2)若cos θ＝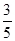
，θ∈
，求f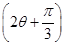
.
在△ABC中，a＝3，b＝2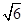
，∠B＝2∠A.
(1)求cos A的值；
(2)求c的值．
函数f(x)＝Asin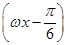 
＋1(A＞0，ω＞0)的最大值为3，其图象相邻两条对称轴之间的距离为
.
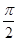(1)求函数f(x)的解析式；
(2)设α∈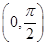
，f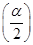
＝2，求α的值．
某村庄拟修建一个无盖的圆柱形蓄水池(不计厚度)．设该蓄水池的底面半径为r米，高为h米，体积为V立方米．假设建造成本仅与表面积有关，侧面积的建造成本为100元/平方米，底面的建造成本为160元/平方米，该蓄水池的总建造成本为12 000π元(π为圆周率)．
(1)将V表示成r的函数V(r)，并求该函数的定义域；
(2)讨论函数V(r)的单调性，并确定r和h为何值时该蓄水池的体积最大．
已知函数f(x)＝x2＋xsin x＋cos x.
(1)若曲线y＝f(x)在点(a，f(a))处与直线y＝b相切，求a与b的值；
(2)若曲线y＝f(x)与直线y＝b有两个不同交点，求b的取值范围．