(本小题满分12分).已知函数 (
(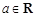 ).
).
(1)若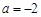 ,求曲线
,求曲线 在点
在点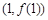 处的切线方程;
处的切线方程;
(2)若不等式 对任意
对任意 恒成立.
恒成立.
(ⅰ)求实数 的取值范围;
的取值范围;
(ⅱ)试比较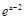 与
与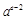 的大小,并给出证明(
的大小,并给出证明(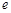 为自然对数的底数,
为自然对数的底数, ).
).
选修4-5:不等式选讲
已知 ,
, .
.
(1)求证: ,
, ;
;
(2)若 ,求证:
,求证: .
.
选修4-4:坐标系与参数方程
已知直线 的参数方程是
的参数方程是 ,圆C的极坐标方程为
,圆C的极坐标方程为 .
.
(1)求圆心C的直角坐标;
(2)由直线 上的点向圆C引切线,求切线长的最小值.
上的点向圆C引切线,求切线长的最小值.
选修4—1:几何证明选讲
如图,AB、CD是圆的两条平行弦,BE//AC,BE交CD于E、交圆于F,过A点的切线交DC的延长线于P,PC=ED=1,PA=2.
(1)求AC的长;
(2)求证:BE=EF.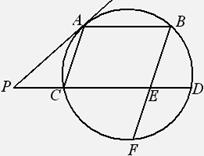
已知函数 在点
在点 处的切线方程为
处的切线方程为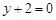 .
.
(1)求函数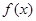 的解析式;
的解析式;
(2)若经过点 可以作出曲线
可以作出曲线 的三条切线,求实数
的三条切线,求实数 的取值范围.
的取值范围.
一个三棱柱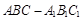 的直观图和三视图如图所示(主视图、俯视图都是矩形,左视图是直角三角形),设
的直观图和三视图如图所示(主视图、俯视图都是矩形,左视图是直角三角形),设 为线段
为线段 上的点.
上的点.
(1)求几何体 的体积;
的体积;
(2)是否存在点E,使平面 平面
平面 ,若存在,求AE的长.
,若存在,求AE的长.