【原创】(本小题满分12分)如图,在三棱锥 中,
中, 底面ABC,
底面ABC, ,AP=AC, 点
,AP=AC, 点 ,
, 分别在棱
分别在棱 上,且BC//平面ADE.
上,且BC//平面ADE.
(Ⅰ)求证:DE⊥平面 ;
;
(Ⅱ)若PC⊥AD,且三棱锥 的体积为8,求多面体ABCED的体积.
的体积为8,求多面体ABCED的体积.
(本小题满分15分)如图,在直三棱柱 中,平面
中,平面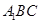
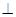 侧面
侧面 且
且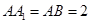 .
.
(Ⅰ)求证: ;
;
(Ⅱ)若直线AC与平面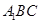 所成的角为
所成的角为 ,求锐二面角
,求锐二面角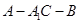 的大小.
的大小.
(本小题满分15分)设数列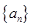 为等差数列,且
为等差数列,且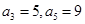 ;数列
;数列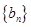 的前
的前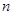 项和为
项和为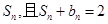 .
.
(Ⅰ)求数列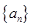 ,
,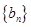 的通项公式;
的通项公式;
(Ⅱ)若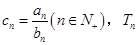 为数列
为数列 的前
的前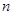 项和,求
项和,求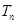 .
.
(本小题满分15分)已知 ,且
,且 ,设
,设 ,
, 的图象相邻两对称轴之间的距离等于
的图象相邻两对称轴之间的距离等于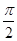 .
.
(Ⅰ)求函数 的解析式;
的解析式;
(Ⅱ)在△ABC中,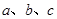 分别为角
分别为角 的对边,
的对边, ,
,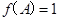 ,求
,求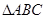 面积的最大值.
面积的最大值.
(本小题满分14分)已知函数 .
.
(Ⅰ)若函数 的图象在
的图象在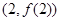 处的切线斜率为
处的切线斜率为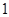 ,求实数
,求实数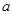 的值;
的值;
(Ⅱ)在(Ⅰ)的条件下,求函数 的单调区间;
的单调区间;
(Ⅲ)若函数 在
在 上是减函数,求实数
上是减函数,求实数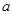 的取值范围.
的取值范围.
(本小题满分15分)已知数列 ,
, 满足
满足 ,
, ,且对任意的正整数
,且对任意的正整数 ,
, 和
和 均成等差数列.
均成等差数列.
(Ⅰ)求 、
、 的值;
的值;
(Ⅱ)证明: 和
和 均成等比数列;
均成等比数列;
(Ⅲ)是否存在唯一正整数 ,使得
,使得 恒成立?证明你的结论.
恒成立?证明你的结论.