（本小题满分12分）
某单位建造一间地面面积为12 平方米的背面靠墙的矩形小房,由于地理位置的限制,房子侧面的长度x不得超过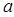
米 ,房屋正面的造价为400元/平方米,房屋侧面的造价为150元/平方米,屋顶和地面的造价费用合计为5800元,如果墙高为3米,且不计房屋背面的费用.(1)把房屋总造价y表示成x的函数,并写出该函数的定义域;(2)当侧面的长度为多少时,总造价最低?最低造价是多少?
（本小题满分12分）已知函数
，
．
（1）判断
在区间
上单调性；
（2）若
，函数
在区间上的最大值为
，求的解析式，并判断是否有最大值和最小值，请说明理由（参考数据：
）．
（本小题满分12分）已知函数
．
（1）若函数
在
上是单调函数，求实数
的取值范围；
（2）已知函数
，对于任意
，总存在
，使得
成立，求正实数的取值范围．
（本小题满分12分）已知函数
以
为切点的切线方程是
．
（1）求实数
，
的值；
（2）若方程
在
上有两个不等实根，求实数
的取值范围．
（本小题满分12分）已知向量
，
．
（1）当
时，求
的值；
（2）设函数
，已知在
中，内角
、
、
的对边分别为
、
、
，若
，
，
，求当
时，
的取值范围．
（本小题满分12分）设命题
函数
的值域为
；命题
不等式
对一切
均成立．
（1）如果
是真命题，求实数
的取值范围；
（2）如果命题“
”为真命题，且“
”为假命题，求实数的取值范围．