(本小题满分10分)选修4-1:几何证明选讲
如图,AB是圆O的直径,C是半径OB的中点,D是OB延长线上一点,且BD=OB,直线MD与圆O相交于点M、T(不与A、B重合),DN与圆O相切于点N,连结MC,MB,OT.
(1)求证: ;
;
(2)若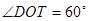 ,试求
,试求 的大小.
的大小.
已知函数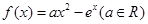
(Ⅰ)当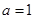 时,判断函数
时,判断函数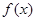 的单调区间并给予证明;
的单调区间并给予证明;
(Ⅱ)若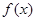 有两个极值点
有两个极值点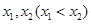 ,证明:
,证明: .
.
已知A、B是椭圆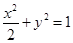 上的两点,且
上的两点,且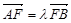 ,其中F为椭圆的右焦点.
,其中F为椭圆的右焦点.
(1)求实数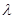 的取值范围;
的取值范围;
(2)在x轴上是否存在一个定点M,使得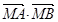 为定值?若存在,求出定值和定点坐标;若不存在,说明理由.
为定值?若存在,求出定值和定点坐标;若不存在,说明理由.
为适应2012年3月23日公安部交通管理局印发的《加强机动车驾驶人管理指导意见》,某驾校将小型汽车驾照考试科目二的培训测试调整为:从10个备选测试项目中随机抽取4个,只有选中的4个项目均测试合格,科目二的培训才算通过.已知甲对10个测试项目测试合格的概率均为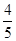 ;乙对其中8个测试项目完全有合格把握,而另2个测试项目却根本不会.
;乙对其中8个测试项目完全有合格把握,而另2个测试项目却根本不会.
(Ⅰ)求甲恰有2个测试项目合格的概率;
(Ⅱ)记乙的测试项目合格数为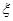 ,求
,求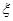 的分布列及数学期望
的分布列及数学期望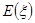 .
.
如图,三棱柱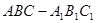 侧棱与底面垂直,且所有棱长都为4,D为CC1中点.
侧棱与底面垂直,且所有棱长都为4,D为CC1中点.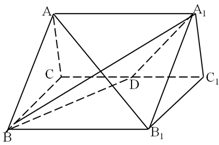
(1)求证: ;
;
(2)求二面角 的余弦值.
的余弦值.