(本小题满分12分)已知 向量
向量 ,
, ,
,
向量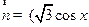 ,
,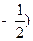 ,函数
,函数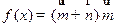 .
.
(Ⅰ)求 的最小正周期
的最小正周期 ;
;
(Ⅱ)已知 ,
,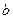 ,
,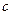 分别为
分别为 内角
内角 ,
,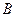 ,
,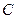 的对边,
的对边, 为锐角,
为锐角, ,
, ,且
,且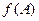 恰是
恰是 在
在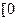 ,
,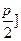 上的最大值,求
上的最大值,求 ,
,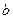 和
和 的面积
的面积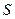 .
.
已知数列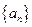 的前
的前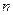 项和
项和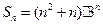 .
.
(Ⅰ)求 ;(Ⅱ)证明:
;(Ⅱ)证明: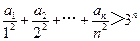 .
.
从四名男生和三名女生中任选3人参加演讲比赛.
(Ⅰ)求所选3人中至少有一名女生的概率;
(Ⅱ) 表示所选参加演讲比赛的人员中男生的人数,求
表示所选参加演讲比赛的人员中男生的人数,求 的分布列和数学期望.
的分布列和数学期望.
(12分)在△ABC中,∠A、∠B、∠C对边分别为a、b、c,已知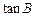 =
= ,且最长边为
,且最长边为
(1)求角A; (2)求△ABC最短边的长.
(本小题满分12分)
已知函数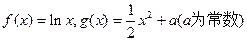 ,直线l与函数
,直线l与函数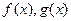 的图象都相切,且l与函数
的图象都相切,且l与函数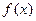 的图象的切点的横坐标为1。
的图象的切点的横坐标为1。
(1)求直线l的方程以及a的值;
(2)若 的单调递增区间.
的单调递增区间.
(本小题满分12分)
某市旅游部门开发一种旅游纪念品,每件产品的成本是15元,销售价是20元,月平均销售a件,通过改进工艺,产品的成本不变,质量和技术含金量提高,市场分析的结果表明,如果产品的销售价提高的百分率为
 ,那么月平均销售量减少的百分率为
,那么月平均销售量减少的百分率为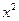 .记改进工艺后,旅游部门销售该纪念品的月平均利润是
.记改进工艺后,旅游部门销售该纪念品的月平均利润是 (元).
(元).
(Ⅰ)写出 与
与 的函数关系式;
的函数关系式;
(Ⅱ)改进工艺后,确定该纪念品的售价,使旅游部门销售该纪念品的月平均利润最大.