(本小题满分14分)已知圆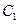 :
: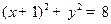 ,点
,点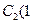 ,
,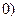 ,点
,点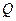 在圆
在圆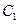 上运动,
上运动,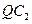 的垂直平分线交
的垂直平分线交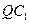 于点
于点 .
.
(Ⅰ)求动点 的轨迹
的轨迹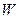 的方程;
的方程;
(Ⅱ)设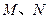 分别是曲线
分别是曲线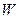 上的两个不同点,且点
上的两个不同点,且点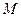 在第一象限,点
在第一象限,点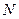 在第三象限,若
在第三象限,若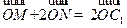 ,
,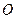 为坐标原点,求直线
为坐标原点,求直线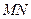 的斜率
的斜率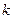 ;
;
(Ⅲ)过点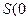 ,
,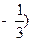 且斜率为
且斜率为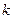 的动直线
的动直线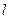 交曲线
交曲线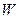 于
于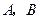 两点,在
两点,在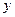 轴上是否存在定点
轴上是否存在定点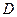 ,使以
,使以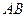 为直径的圆恒过这个点?若存在,求出
为直径的圆恒过这个点?若存在,求出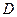 的坐标,若不存在,说明理由.
的坐标,若不存在,说明理由.
已知函数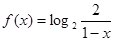 .
.
(Ⅰ)求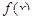 的定义域
的定义域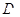 及其零点;
及其零点;
(Ⅱ)判断函数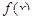 在定义域
在定义域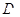 上的单调性,并用函数单调性定义证明.
上的单调性,并用函数单调性定义证明.
(Ⅰ)求值: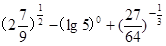
(Ⅱ)求值: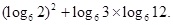
已知定义域为R的函数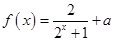 是奇函数,
是奇函数,
(1)求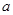 的值.
的值.
(2)判断函数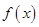 在
在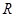 上的单调性并加以证明;
上的单调性并加以证明;
(3)若对于任意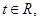 不等式
不等式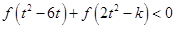 恒成立,求
恒成立,求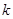 的取值范围.
的取值范围.
已知函数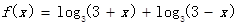 .
.
(1)求函数f(x)的定义域和值域;
(2)判断函数f(x)的奇偶性,并说明理由.
邵东某桶装水经营部每天的房租、人员工资等固定成本为360元,每桶水进价4元,销售单价与日均销量的关系如表所示
| 销售单价/元 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
| 日均销售量/桶 |
360 |
320 |
280 |
240 |
200 |
160 |
120 |
请根据以上数据作出分析,这个经营部怎样定价(单价要为整元)才能获得最大利润?最大利润为多少?