邵东某桶装水经营部每天的房租、人员工资等固定成本为360元,每桶水进价4元,销售单价与日均销量的关系如表所示
| 销售单价/元 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
| 日均销售量/桶 |
360 |
320 |
280 |
240 |
200 |
160 |
120 |
请根据以上数据作出分析,这个经营部怎样定价(单价要为整元)才能获得最大利润?最大利润为多少?
已知函数 .
.
(1)证明: ;
;
(2)当 时,
时, ,求
,求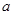 的取值范围.
的取值范围.
已知抛物线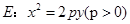 ,直线
,直线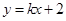 与E交于A、B两点,且
与E交于A、B两点,且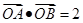 ,其中O为原点.
,其中O为原点.
(1)求抛物线E的方程;
(2)点C坐标为 ,记直线CA、CB的斜率分别为
,记直线CA、CB的斜率分别为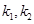 ,证明:
,证明: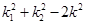 为定值.
为定值.
据民生所望,相关部门对所属服务单位进行整治行核查,规定:从甲类3个指标项中随机抽取2项,从乙类2个指标项中随机抽取1项.在所抽查的3个指标项中,3项都优秀的奖励10万元;只有甲类2项优秀的奖励6万元;甲类只有1项优秀、乙类1项优秀的提出警告,有2项或2项以上不优秀的停业运营并罚款8万元.已知某家服务单位甲类3项指标项中有2项优秀,乙类2项指标项中有1项优秀.
求:(1)这家单位受到奖励的概率;
(2)这家单位这次整治性核查中所获金额的均值(奖励为正数,罚款为负数).
如图,在三棱锥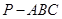 中,
中,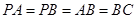 ,
,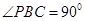 ,D为AC的中点,
,D为AC的中点,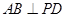 .
.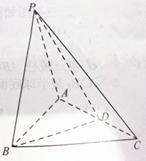
(1)求证:平面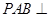 平面
平面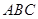 ;
;
(2)如果三棱锥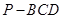 的体积为3,求
的体积为3,求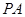 .
.
在锐角 中,
中,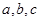 分别为角
分别为角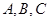 的对边,且
的对边,且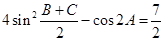 .
.
(1)求角A的大小;
(2)求 的最大值.
的最大值.