(本小题满分12分)
改革开放以来,我国高等教育事业有了突飞猛进的发展,有人记录了某村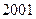 到
到 年十年间每年考入大学的人数.
年十年间每年考入大学的人数. 为方便计算,
为方便计算,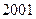 年编号为
年编号为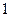 ,
, 年编号为
年编号为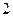 ,…,
,…, 年编号为
年编号为 .数据如下:
.数据如下: 
(Ⅰ)从这 年中随机抽取两年,求考入大学人数至少有
年中随机抽取两年,求考入大学人数至少有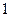 年多于
年多于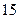 人的概率;
人的概率;
(Ⅱ)根据前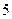 年的数据,利用最小二乘法求出
年的数据,利用最小二乘法求出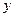 关于
关于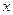 的回归方程
的回归方程 ,并计算第
,并计算第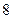 年的估计值和实际值之间的差的绝对值.
年的估计值和实际值之间的差的绝对值.
(本小题满分12分)银川市有甲,乙两家室内羽毛球馆,两家设备和服务都相当,但收费方式不同.甲羽毛球馆每小时50元;乙羽毛球馆按月计费,一个月中30小时以内(含30小时)900元,超过30小时的部分每小时20元.肖老师为了锻炼身体,准备下个月从这两家羽毛球馆中选择一家进行健身活动,其活动时间不少于15小时,也不超过40小时.设甲羽毛球馆健身 小时的收费为
小时的收费为 元,乙羽毛球馆健身
元,乙羽毛球馆健身 小时的收费为
小时的收费为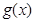 元.
元.
(Ⅰ)当 时,分别写出函数
时,分别写出函数 和
和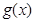 的表达式;
的表达式;
(Ⅱ)请问肖老师选择哪家羽毛球馆健身比较合算?为什么?
(本小题满分12分)已知函数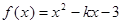 ,
,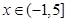 .
.
(Ⅰ)当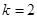 时,求函数
时,求函数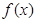 的值域;
的值域;
(Ⅱ)若函数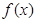 在区间
在区间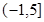 上是单调函数,求实数
上是单调函数,求实数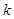 的取值范围.
的取值范围.
(本小题满分12分)已知函数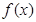 是定义在
是定义在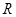 上的偶函数.若
上的偶函数.若 时,
时,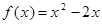 .
.
(Ⅰ)当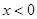 时,求函数
时,求函数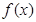 的解析式;
的解析式;
(Ⅱ)画出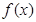 的简图;(要求绘制在答题卷的坐标纸上);
的简图;(要求绘制在答题卷的坐标纸上);
(Ⅲ)结合图像写出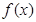 的单调区间(只写结论,不用证明).
的单调区间(只写结论,不用证明).
(本小题满分12分)已知函数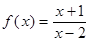 ,其中
,其中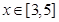 .
.
(Ⅰ)用定义证明函数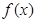 在
在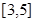 上单调递减;
上单调递减;
(Ⅱ)结合单调性,求函数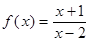 在区间
在区间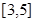 上的最大值和最小值.
上的最大值和最小值.
(本小题满分10分)已知集合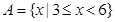 ,
,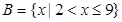 .
.
(Ⅰ)求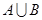 ,
,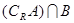 ;
;
(Ⅱ)已知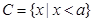 ,若
,若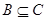 ,求实数
,求实数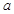 的取值范围.
的取值范围.