(本小题满分10分)选修4-1:几何证明选讲
如图,直线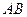 经过⊙
经过⊙ 上的点
上的点 ,并且
,并且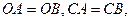 ⊙
⊙ 交直线
交直线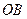 于
于 ,
,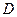 ,连接
,连接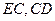 .
.
(Ⅰ)求证:直线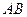 是⊙
是⊙ 的切线;
的切线;
(Ⅱ)若 ⊙
⊙ 的半径为
的半径为 ,求
,求 的长.
的长.
在平面直角坐标系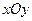 中,已知三点
中,已知三点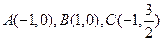 ,以A、B为焦点的椭圆经过点C。
,以A、B为焦点的椭圆经过点C。
(Ⅰ)求椭圆的方程;
(Ⅱ)设点D(0,1),是否存在不平行于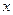 轴的直线
轴的直线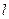 椭圆交于不同两点M、N,使
椭圆交于不同两点M、N,使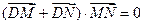 ?若存在
?若存在 ,求出直线
,求出直线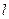
 斜率的取值范围;若不存在,请说
斜率的取值范围;若不存在,请说 明理由;
明理由;
(Ⅲ)对于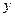 轴上的点
轴上的点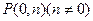 ,存在不平等于
,存在不平等于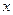 轴的直线
轴的直线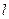 与椭圆交于不同两点M、N,使
与椭圆交于不同两点M、N,使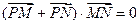 ,试求实数
,试求实数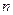 的
的 取值范围。
取值范围。
12分)
已知二次函数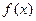 的二次项系数为a,且不等式
的二次项系数为a,且不等式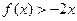 的解集为(1,3)。
的解集为(1,3)。
(1) 若方程
若方程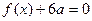 有两个相等的实数根,求
有两个相等的实数根,求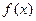 的解析式;
的解析式;
(2)若函数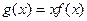 无极值,求实数
无极值,求实数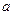 的取值范围。
的取值范围。
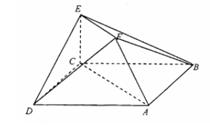
在如图所示的多面体中,已知正方形ABCD和直角梯形ACEF所在的平面互相垂直,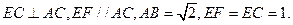
(Ⅰ)求证:平面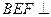 平
平 面DEF;
面DEF;
(Ⅱ)求二面 角A—BF—E的大小。
角A—BF—E的大小。
某项选拔共有四轮考核,每轮设有一个问题,能正确回答问题者进入下一轮考核,否则即被淘汰。已知某选手能正确回答第一、二、三、四轮的问题的概率分别为 且各轮问题能否正确回答互不影响。
且各轮问题能否正确回答互不影响。
(Ⅰ)求该选手进入第四轮才被淘汰的概率;
(Ⅱ)求该选手至多进入第三轮考核的概率
已知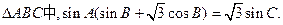
(Ⅰ)求角A的大小 ;
;
(Ⅱ)若BC=3,求 周长的取值范围。
周长的取值范围。