已知曲线C的参数方程为(α∈R,α为参数).当极坐标系的极点与直角坐标系的原点重合,且极轴 在x轴的正半轴上时,曲线D的极坐标力程为ρsin(θ+)=a.
在x轴的正半轴上时,曲线D的极坐标力程为ρsin(θ+)=a.
(I)、试将曲线C的方程化为普通方程,曲线D的方程化为直角坐标方程;
(II)、试确定实数a的取值范围,使曲 线C与曲线D有公共点.
线C与曲线D有公共点.
已知椭圆 左、右焦点分别为F1、F2,点P(2,
左、右焦点分别为F1、F2,点P(2,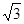 ),点F2在线段PF1的中垂线上.
),点F2在线段PF1的中垂线上.
(1)求椭圆C的方程;
(2)设直线 与椭圆C交于M、N两点,直线F2M与F2N的斜率互为相反数,求证:直线l过定点,并求该定点的坐标.
与椭圆C交于M、N两点,直线F2M与F2N的斜率互为相反数,求证:直线l过定点,并求该定点的坐标.
如图,在四棱锥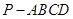 中,底面
中,底面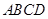 为矩形,侧棱
为矩形,侧棱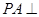 底面
底面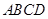 ,
,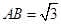 ,
,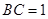 ,
,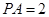 ,
, 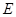 为
为 的中点.
的中点.
(1)求直线 与
与 所成角的余弦值;
所成角的余弦值;
(2)在侧面 内找一点
内找一点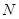 ,使
,使 面
面 ,并求出点
,并求出点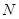 到
到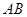 和
和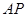 的距离.
的距离.
在平面直角坐标系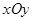 中,已知动点
中,已知动点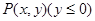 到点
到点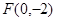 的距离为
的距离为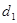 ,到
,到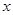 轴的距离为
轴的距离为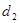 ,且
,且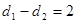 .
.
(1)求点 的轨迹
的轨迹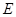 的方程;
的方程;
(2) 若直线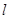 斜率为1且过点
斜率为1且过点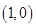 ,其与轨迹
,其与轨迹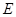 交于点
交于点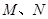 ,求
,求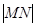 的值.
的值.
已知命题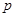 :方程
:方程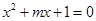 有两个不等的负实根,命题
有两个不等的负实根,命题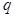 :方程
:方程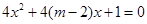 无实根。若
无实根。若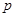 或
或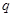 为真,
为真,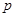 且
且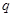 为假。求实数
为假。求实数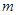 的取值范围.
的取值范围.
已知点A(3,2), 点P是抛物线y2=4x上的一个动点,F为抛物线的焦点,求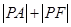 的最小值及此时P点的坐标.
的最小值及此时P点的坐标.