已知椭圆C的中心在原点,焦点在x轴上,左右焦点分别为F1,F2;且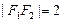
点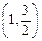 在椭圆C上.
在椭圆C上.
(1)求椭圆C的方程;
(2)过F1的直线l与椭圆C相交于A、B两点,且△AF2B的面积为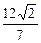 ,求以F2为圆
,求以F2为圆
心且与直线l相切的圆的方程.
如图是在竖直平面内的一个“通道游戏”.图中竖直线段和斜线段都表示通道,并且在交点处相遇,若竖直线段有一条的为第一层,有二条的为第二层, ,依次类推.现有一颗小弹子从第一层的通道里向下运动,若在通道的分叉处,小弹子以相同的概率落入每个通道.记小弹子落入第 层第
层第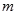 个竖直通道(从左至右)的概率为
个竖直通道(从左至右)的概率为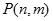 ,某研究性学习小组经探究发现小弹子落入第
,某研究性学习小组经探究发现小弹子落入第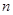 层的第
层的第 个通道的次数服从二项分布,请你解决下列问题.
个通道的次数服从二项分布,请你解决下列问题.
(Ⅰ)试求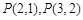 及
及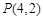 的值,并猜想
的值,并猜想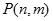 的表达式;(不必证明)
的表达式;(不必证明)
(Ⅱ)设小弹子落入第6层第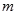 个竖直通道得到分数为
个竖直通道得到分数为 ,其中
,其中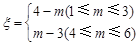 ,试求
,试求 的分布列及数学期望.
的分布列及数学期望.
如图,在长方体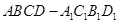 中,已知上下两底面为正方形,且边长均为1;侧棱
中,已知上下两底面为正方形,且边长均为1;侧棱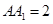 ,
,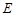 为
为 中点,
中点, 为
为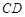 中点,
中点,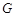 为
为 上一个动点.
上一个动点.
(Ⅰ)确定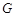 点的位置,使得
点的位置,使得 ;
;
(Ⅱ)当 时,求二面角
时,求二面角 的平面角余弦值.
的平面角余弦值.
已知等差数列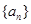 的首项
的首项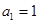 ,公差
,公差 .且
.且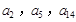 分别是等比数列
分别是等比数列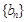 的
的 .
.
(Ⅰ)求数列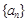 与
与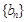 的通项公式;
的通项公式;
(Ⅱ)设数列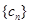 对任意自然数
对任意自然数 均有
均有
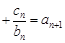 成立,求
成立,求
 的值.
的值.
已知A、B、C为 的三个内角且向量
的三个内角且向量 与
与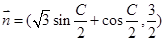 共线.
共线.
(Ⅰ)求角C的大小;
(Ⅱ)设角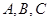 的对边分别是
的对边分别是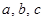 ,且满足
,且满足 ,试判断
,试判断
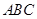 的形状.
的形状.
设 .
.
(1)解不等式 ;
;
(2)若对任意实数 ,
, 恒成立,求实数a的取值范围.
恒成立,求实数a的取值范围.