如图，是一个用六根竹条连接而成的凸六边形风筝骨架，考虑到骨架-优题课

如图，是一个用六根竹条连接而成的凸六边形风筝骨架，考虑到骨架的稳固性、美观性、实用性等因素，需再加竹条与其顶点连接。要求：

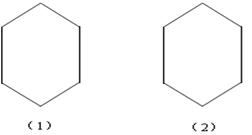
（1）在图（1）、（2）中分别加适当根竹条，设计出两种不同的连接方案。
（2）通过上面的设计，可以看出至少需再加根竹条，才能保证风筝骨架稳固、美观和实用。（3）在上面的方案设计过程中，你所应用的数学道理是

科目数学题型解答题难度中等

知识点：三角形的五心

（1）如图①，点 $A$ 是 $⊙ O$ 外一点，点 $P$ 是 $⊙ O$ 上一动点．若 $⊙ O$ 的半径为3，且 $OA = 5$ ，则点 $P$ 到点 $A$ 的最短距离为　；

（2）如图②，已知正方形 $ABCD$ 的边长为4，点 $M$ 、 $N$ 分别从点 $B$ 、 $C$ 同时出发，以相同的速度沿边 $BC$ 、 $CD$ 方向向终点 $C$ 和 $D$ 运动，连接 $AM$ 和 $BN$ 交于点 $P$ ，则点 $P$ 到点 $C$ 的最短距离为　　；

（3）如图③，在等边 $ΔABC$ 中， $AB = 6$ ，点 $M$ 、 $N$ 分别从点 $B$ 、 $C$ 同时出发，以相同的速度沿边 $BC$ 、 $CA$ 方向向终点 $C$ 和 $A$ 运动，连接 $AM$ 和 $BN$ 交于点 $P$ ，求 $ΔAPB$ 面积的最大值，并说明理由．

如图，已知抛物线 $L : y = a x^{2} + bx + c (a \neq 0)$ 与 $x$ 轴交于 $A$ 、 $B$ 两点．与 $y$ 轴交于 $C$ 点．且 $A (- 1, 0)$ ， $OB = OC = 3 OA$ ．

（1）求抛物线 $L$ 的函数表达式；

（2）在抛物线 $L$ 的对称轴上是否存在一点 $M$ ，使 $ΔACM$ 周长最小？若存在，求出点 $M$ 的坐标；若不存在，请说明理由．

（3）连接 $AC$ 、 $BC$ ，在抛物线 $L$ 上是否存在一点 $N$ ，使 $S_{ΔABC} = 2 S_{ΔOCN}$ ？若存在，求出点 $N$ 的坐标；若不存在，请说明理由．

如图， $ΔABC$ 为 $⊙ O$ 的内接三角形， $∠ ABC$ 的角平分线交 $⊙ O$ 于点 $D$ ，过点 $D$ 作 $DE / / AC$ 交 $BC$ 的延长线于点 $E$ ．

（1）求证： $DE$ 为 $⊙ O$ 的切线；

（2）若 $DE = \frac{1}{2} AC$ ，求 $∠ ACB$ 的大小．

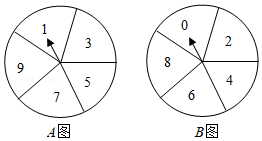
小明的爸爸买了一个密码旅行箱，密码由六位数字组成．现小明爸爸已将密码的前四位数字确定为小明的生日 $(1028)$ ，后两位数字由小明自己确定．小明想把十位上的数字设置为奇数，个位上的数字设置为偶数，且两个数位上的数字之和为9．这两个数位上的数字他采用转转盘的方式来确定，于是，小明设计了如图所示的两个可以自由转动的转盘 $A$ 和 $B$ （每个转盘被分成五个面积相等的扇形区域）．使用的规则如下：

同时转动两个转盘，转盘均停正后，记下两个指针所指扇形区域上的数（如果指针指到分割线上，那么就取指针右边扇形区域上的数）．若记下的两个数之和为9，则确定为密码中的数字；否则，按上述规则继续转动两个转盘，直到记下的两个数之和为9为止．请用列表法或画树状图的方法，求小明同时转动两个转盘一次，得到的两个数之和恰好为9的概率．

某樱桃种植户有20吨樱桃待售，现有两种销售方式：一是批发，二是零售．经过市场调查，这两种销售方式对这个种植户而言，每天的销量及每吨所获的利润如下表：

销售方式	每天销量（吨 $)$	每吨所获利润（元 $)$
批发	3	4000
零售	1	6000

假设该种植户售完20吨樱桃，共批发了 $x$ 吨，所获总利润为 $y$ 元．

（1）求出 $y$ 与 $x$ 之间的函数关系式；

（2）若受客观因素影响，这个种植户每天只能采用一种销售方式销售，且正好10天销售完所有樱桃，请计算该种植户所获总利润是多少元？