(本小题满分12分)
已知梯形 中,
中, ∥
∥ ,
, ,
, ,
, 、
、 分别是
分别是 上的点,
上的点, ∥
∥ ,
, ,
, 是
是 的中点。沿
的中点。沿 将梯形
将梯形 翻折,使平面
翻折,使平面 ⊥平面
⊥平面 (如图) .
(如图) .
(Ⅰ)当 时,求证:
时,求证: ;
;
(Ⅱ)以 为顶点的三棱锥的体积记为
为顶点的三棱锥的体积记为 ,求
,求 的最大值;
的最大值;
(Ⅲ)当 取得最大值时,求钝二面角
取得最大值时,求钝二面角 的余弦值.
的余弦值.
(本小题满分12分)
某社区为了选拔若干名2010年上海世博会的义务宣传员,从社区300名志愿者中随机抽取了50名进行世博会有关知识的测试,成绩(均为整数)按分数段分成六组: 第一组 ,第二组
,第二组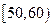 ,
, ,第六组
,第六组 ,第一、二、三组的人数依次构成等差数列,右图是按上述分组方法得到的频率分布直方图的一部分.规定成绩不低于66分的志愿者入选为义务宣传员.
,第一、二、三组的人数依次构成等差数列,右图是按上述分组方法得到的频率分布直方图的一部分.规定成绩不低于66分的志愿者入选为义务宣传员.
(1)求第二组、第三组的频率并补充完整频率分布直方图;
(2)由所抽取志愿者的成绩分布,估计该社区有多少志愿者可以入选为义务宣传员.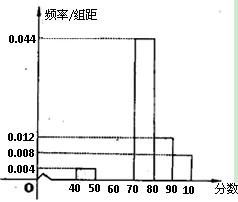
(本小题满分12分)
在 中,角A、B、C的对边分别为
中,角A、B、C的对边分别为 ,已知
,已知 ,且
,且
(1)求角C的大小;
(2)求 ABC的面积.
ABC的面积.
(本小题满分10分4—5不等式选讲)
已知对于任意非零实数 ,不等式
,不等式 恒成立,求实数
恒成立,求实数 的取值范围。
的取值范围。
(本小题满分10分,选修4—4坐标系与参数方程选讲)
已知曲线C的极坐标方程为 ,
,
(1)求曲线C的直角坐标方程.
(2)若P( )是曲线C上的一动点,求
)是曲线C上的一动点,求 的最大值。
的最大值。
(本小题满分10分,选修4—1几何证明选讲)
如图,AB是⊙O的直径,C,F是⊙O上的点,OC垂直于直径AB,过F点作⊙O的切线交AB的延长线于 D.连结CF交AB于E点.
(1)求证: ;
;
(2)若⊙O的半径为 ,OB=
,OB= OE,求EF的长.
OE,求EF的长.