我们常用的数是十进制数,计算机程序使用的是二进制数(只有数码0和1),它们两者之间可以互相换算,如将(101) ,(1011)
,(1011)  换算成十进制数为:
换算成十进制数为:
(101)  =1×2
=1×2 +0×2
+0×2 +1=4+0+1=5;(1011)
+1=4+0+1=5;(1011)  =1×2
=1×2 +0×2
+0×2 +1×2
+1×2 +1=11;
+1=11;
两个二进制数可以相加减,相加减时,将对应数位上的数相加减.与十进制中的“逢十进一”、“退一还十”相类似,应用“逢二进一”、“退一还二”的运算法则,如: (101)  +(11)
+(11)  ="(1000)"
="(1000)"  ;(110)
;(110)  +(11)
+(11)  ="(11)"
="(11)"  ,用竖式运算如右侧所示.(12分)
,用竖式运算如右侧所示.(12分)
(1)按此方式,将二进制(1001)2换算成十进制数的结果是 ▲ .
(2)计算:(10101)  +(111)
+(111)  = ▲ (结果仍用二进制数表示);
= ▲ (结果仍用二进制数表示);
(110010)  -(1111)
-(1111)  = ▲ (结果用十进制数表示).
= ▲ (结果用十进制数表示).
如图,在 的方格纸中,线段 的端点均在格点上,请按要求画图.
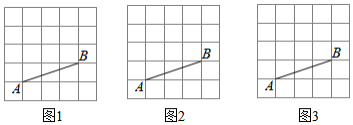
(1)如图1,画出一条线段 ,使 , 在格点上;
(2)如图2,画出一条线段 ,使 , 互相平分, , 均在格点上;
(3)如图3,以 , 为顶点画出一个四边形,使其是中心对称图形,且顶点均在格点上.
在创建"浙江省健康促进学校"的过程中,某数学兴趣小组针对视力情况随机抽取本校部分学生进行调查,并按照国家分类标准统计人数,绘制成两幅不完整的统计图表,请根据图表信息解答下列问题:
抽取的学生视力情况统计表
|
类别 |
检查结果 |
人数 |
|
|
正常 |
88 |
|
|
轻度近视 |
▲ |
|
|
中度近视 |
59 |
|
|
重度近视 |
▲ |
(1)求所抽取的学生总人数;
(2)该校共有学生约1800人,请估算该校学生中,近视程度为中度和重度的总人数;
(3)请结合上述统计数据,为该校做好近视防控,促进学生健康发展提出一条合理的建议.

计算: .
在平面直角坐标系中,点 的坐标为 , ,点 在直线 上,过点 作 的垂线,过原点 作直线 的垂线,两垂线相交于点 .
(1)如图,点 , 分别在第三、二象限内, 与 相交于点 .
①若 ,求证: .
②若 ,求四边形 的面积.
(2)是否存在点 ,使得以 , , 为顶点的三角形与 相似?若存在,求 的长;若不存在,请说明理由.

背景:点 在反比例函数 的图象上, 轴于点 , 轴于点 ,分别在射线 , 上取点 , ,使得四边形 为正方形.如图1,点 在第一象限内,当 时,小李测得 .
探究:通过改变点 的位置,小李发现点 , 的横坐标之间存在函数关系.请帮助小李解决下列问题.
(1)求 的值.
(2)设点 , 的横坐标分别为 , ,将 关于 的函数称为" 函数".如图2,小李画出了 时" 函数"的图象.
①求这个" 函数"的表达式.
②补画 时" 函数"的图象,并写出这个函数的性质(两条即可).
③过点 作一直线,与这个" 函数"图象仅有一个交点,求该交点的横坐标.
