背景:点 在反比例函数 的图象上, 轴于点 , 轴于点 ,分别在射线 , 上取点 , ,使得四边形 为正方形.如图1,点 在第一象限内,当 时,小李测得 .
探究:通过改变点 的位置,小李发现点 , 的横坐标之间存在函数关系.请帮助小李解决下列问题.
(1)求 的值.
(2)设点 , 的横坐标分别为 , ,将 关于 的函数称为" 函数".如图2,小李画出了 时" 函数"的图象.
①求这个" 函数"的表达式.
②补画 时" 函数"的图象,并写出这个函数的性质(两条即可).
③过点 作一直线,与这个" 函数"图象仅有一个交点,求该交点的横坐标.

解下列方程:
(1)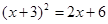 ;(2)
;(2)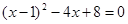
如图,直角梯形ABCD中,AD∥BC,∠A=90o,∠C=60°,AD=3cm,BC=9cm.⊙O的圆心O1从点A开始沿折线A—D—C以1cm/s的速度向点C运动,⊙O2的圆心O2从点B开始沿BA边以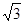 cm/s的速度向点A运动,⊙O1半径为2cm,⊙O2的半径为4cm,若O1、O2分别从点A、点B同时出发,运动的时间为ts.
cm/s的速度向点A运动,⊙O1半径为2cm,⊙O2的半径为4cm,若O1、O2分别从点A、点B同时出发,运动的时间为ts.
(1)请求出⊙O2与腰CD相切时t的值;
(2)在0s<t≤3s范围内,当t为何值时,⊙O1与⊙O2外切? 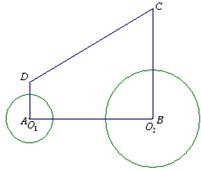
如图,秋千拉绳长AB为3米,静止时踩板离地面0.5米,某小朋友荡该秋千时,秋千在最高处时踩板离地面2米(左右对称),请计算该秋千所荡过的圆弧长?(结果保留π)
连云港市某楼盘准备以每平方米6000元的均价对外销售,由于国务院有关房地产的新政策出台后,购房者持币观望,房地产开发商为了加快资金周转,对价格经过两次下调后,决定以每平方米4860元的均价开盘销售。
(1)求平均每次下调的百分率。
(2)某人准备以开盘价均价购买一套100平方米的住房,开发商给予以下两种优惠方案以供选择:①打9.8折销售;②不打折,一次性送装修费每平方米80元,试问哪种方案更优惠?
如图,直角梯形纸片ABCD中,AD∥BC,∠A=90°,∠C=30°.折叠纸片使BC经过点D.点C落在点E处,BF是折痕,且BF=CF=8.
(l)求∠BDF的度数;
(2)求AB的长.