某食品厂从生产的袋装食品中抽出样品20袋,检测每袋的质量是否符合标准,超过或不足的部分分别用正、负数来表示,记录如下表:
| 与标准质量的差值(单位克) |
-5 |
-2 |
0 |
1 |
3 |
6 |
| 袋数 |
1 |
4 |
3 |
4 |
5 |
3 |
根据上述信息解决如下问题:这批样品的平均质量比标准质量多或少几克?若标准质量为100克,则抽样检测的总质量是多少?
学校计划用地面砖铺设教学楼前矩形广场的地面ABCD已知矩形广场地面的长为100米,宽为80米.图案设计如图所示:广场的四角为小正方形,阴影部分为四个矩形,四个矩形的宽都为小正方形的边长,阴影部分铺绿色地面砖,其余部分铺白色地面砖.
(1)要使铺白色地面砖的面积为5200平方米,则矩形广场四角的小正方形的边长为多少米?
(2)如果铺白色地面砖的费用为每平方米30元,铺绿色地面砖的费用为每平方米20元.当广场四角小正方形的边长为多少米时,铺广场地面的总费用最少?最少费用是多少?
已知:二次函数y=x2+bx-3的图象经过点A(2,5).
(1)求二次函数的解析式;
(2)求二次函数的图象与x轴的交点坐标;
(3)将(1)中求得的函数解析式用配方法化成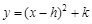 的形式.
的形式.
运用适当的方法解方程
(1)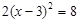
(2)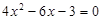
(3)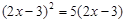
(4)(x+8)(x+1)=-12
(本题满分14分 ,第(1)小题5分,第(2)小题5分,第(3)小题4分)
如图,已知在等腰 Rt△ABC中,∠C=90°,斜边AB=2,若将△ABC翻折,折痕EF分别交边AC、边BC于点E和点F(点E不与A点重合,点F不与B点重合),且点C落在AB边上,记作点D.过点D作DK⊥AB,交射线AC于点K,设AD=x,y=cot∠CFE,


(1)求证:△DEK∽△DFB;
(2)求y关于x的函数解析式并写出定义域;
(3)联结CD,当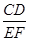 =
= 时,求x的值
时,求x的值
(本题满分12分, 第(1)小题6分,第(2)小题6分)
如图,在平面直角坐标系内,已知直线 与x轴、y轴分别相交于点A和点C,抛物线
与x轴、y轴分别相交于点A和点C,抛物线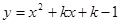 图像过点A和点C,抛物线与x轴的另一交点是B,
图像过点A和点C,抛物线与x轴的另一交点是B,
(1)求出此抛物线的解析式、对称轴以及B点坐标;
(2)若在y轴负半轴上存在点D,能使得以A、C、D为顶点的三角形与△ABC相似,请求出点D的坐标.