已知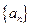 是等差数列,
是等差数列, 是各项为正
是各项为正 数的等比数列,且
数的等比数列,且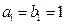 ,
,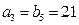 ,
,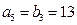 .
.
⑴求通项公式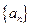 和
和 ;
;
⑵若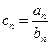 ,求数列
,求数列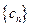 的前
的前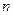 项和
项和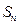 .
.
在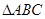 中,
中,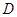 为
为 边上的点
边上的点 ,且
,且 .
.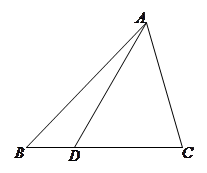
(1)求 ;
;
(2)若 ,求
,求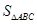 .
.
已知函数
(1)当 时,求
时,求 的极小值;
的极小值;
(2)若直线 对任意的
对任意的 都不是曲线
都不是曲线 的切线,求
的切线,求 的取值范围;
的取值范围;
(3)设 ,求
,求 的最大值
的最大值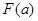 的解析式.
的解析式.
已知 ,
, ,
, .
.
(1)若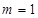 ,
, ,求
,求 的外接圆的方程;
的外接圆的方程;
(2)若以线段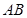 为直径的圆
为直径的圆 过点
过点 (异于点
(异于点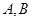 ),直线
),直线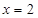 交直线
交直线 于点
于点 ,线段
,线段 的中点为
的中点为 ,试判断直线
,试判断直线 与圆
与圆 的位置关系,并证明你的结论.
的位置关系,并证明你的结论.
数列 的前
的前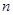 项和为
项和为 ,数列
,数列 是首项为
是首项为 ,公差不为零的等差数列,且
,公差不为零的等差数列,且 成等比数列.
成等比数列.
(1)求 的值;
的值;
(2)求数列 与
与 的通项公式;
的通项公式;
(3)求证:
如图所示,已知圆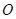 的直径
的直径 长度为4,点
长度为4,点 为线段
为线段 上一点,且
上一点,且 ,点
,点 为圆
为圆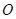 上一点,且
上一点,且 .点
.点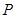 在圆
在圆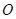 所在平面上的正投影为
所在平面上的正投影为
点 ,
, .
.
(1)求证: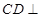 平面
平面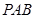 ;
;
(2)求点 到平面
到平面 的距离.
的距离.