((本小题满分12分)
已知数列 是公差为
是公差为 的等差数列,
的等差数列, 为其前
为其前 项和。
项和。
(1)若 ,
, ,
, 依次成等比数列,求其公比
依次成等比数列,求其公比 ;
;
(2)若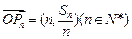 ,求证:对任意的
,求证:对任意的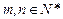 ,向量
,向量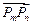 与向量
与向量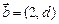 共线;
共线;
(3)若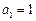 ,
, ,
, ,问是否存在一个半径最小的圆,使得对任意的
,问是否存在一个半径最小的圆,使得对任意的 ,点
,点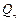 都在这个圆内或圆周上。
都在这个圆内或圆周上。
(本小题12分)在锐角△ABC中,角A,B,C的对边分别为a,b,c,已知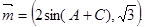 ,
,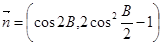 ,且
,且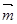 ∥
∥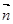
(1)求角B的大小
(2)若b=1,求△ABC面积的最大值
选修4—1:几何问题选讲
如图,已知AB是⊙O的直径,弦CD与AB垂直,垂足为M,E是CD延长线上的一点,且AB=10,CD=8,3DE=4OM,过F点作⊙O的切线EF,BF交CD于G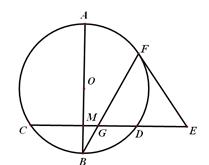
(Ⅰ)求EG的长;
(Ⅱ)连接FD,判断FD与AB是否平行,为什么?
选修4—5:不等式选讲
已知关于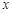 的不等式
的不等式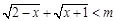 对于任意的
对于任意的 恒成立
恒成立
(Ⅰ)求 的取值范围;
的取值范围;
(Ⅱ)在(Ⅰ)的条件下求函数 的最小值.
的最小值.
选修4—4:极坐标与参数方程
在直角坐标平面内,以坐标原点 为极点,
为极点,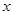 轴的非负半轴为极轴建立极坐标系.已知点
轴的非负半轴为极轴建立极坐标系.已知点 、
、 的极坐标分别为
的极坐标分别为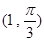 、
、 ,曲线
,曲线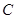 的参数方程为
的参数方程为 为参数).
为参数).
(Ⅰ)求直线 的直角坐标方程;
的直角坐标方程;
(Ⅱ)若直线 和曲线C只有一个交点,求
和曲线C只有一个交点,求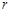 的值.
的值.
(本小题满分12分)已知函数 ,
,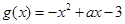 .
.
(Ⅰ)求函数 的极值;
的极值;
(Ⅱ)若对 有
有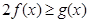 恒成立,求实数
恒成立,求实数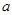 的取值范围..
的取值范围..