(本题满分10分) 选修4—4:坐标系与参数方程
已知曲线C1的极坐标方程为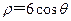 ,曲线C2的极坐标方程为
,曲线C2的极坐标方程为 ,曲线C1,C2相交于点A,B.
,曲线C1,C2相交于点A,B.
(Ⅰ)将曲线C1,C2的极坐标方程化为直角坐标方程;
(Ⅱ)求弦AB的长.
已知函数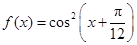 ,
,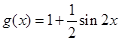 .
.
(1)设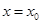 是函数
是函数 图象的一条对称轴,求
图象的一条对称轴,求 的值;
的值;
(2)求函数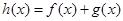 的单调递增区间.
的单调递增区间.
已知A、B、C三点的坐标分别是A(3,0),B(0,3),C ,其中
,其中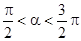 ,
,
(1)若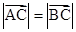 ,求角
,求角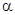 的值;
的值;
(2)若 ,求
,求 的值.
的值.
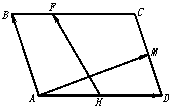
如图,平行四边形ABCD中,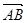 =a,
=a,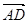 =b,H、M是AD、DC之中点,F使BF=
=b,H、M是AD、DC之中点,F使BF= BC,(1)以a、b为基底表示向量
BC,(1)以a、b为基底表示向量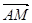 与
与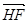 ;(2)若|a|=3,|b|=4,a与b的夹角为
;(2)若|a|=3,|b|=4,a与b的夹角为 ,求
,求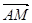

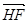 .
.
求值: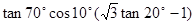
某公司2011年利润为100万元,因市场竞争,若不开发新项目,预测从2012年起每年利润比上一年减少4万元.2012年初,该公司一次性投入90万元开发新项目,预测在未扣除开发所投入资金的情况下,第n年(n为正整数,2012年为第一年)的利润为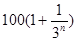 万元.
万元.
(1)设从2012年起的前n年,该公司不开发新项目的累计利润为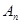 万元,开发新项目的累计利润为
万元,开发新项目的累计利润为 万元(须扣除开发所投入资金),求
万元(须扣除开发所投入资金),求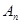 ,
, 的表达式.
的表达式.
(2)依上述预测,该公司从第几年开始,开发新项目的累计利润超过不开发新项目的累计利润?