((本小题满分12分)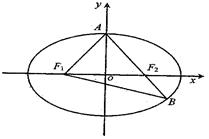
如图,已知椭圆方程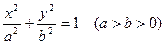 ,
,
F1、F2分别为椭圆的左、右焦点,A为
椭圆的一顶点,直线AF2交椭圆于点B.
(1)若∠F1AB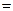 90°,求椭圆的离心率;
90°,求椭圆的离心率;
(2)若椭圆的焦距为2,且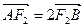 ,
,
求椭圆的方程.
在生产过程中,测得纤维产品的纤度(表示纤维粗细的一种量)共有100个数据,将数据分组如表:
| 分组 |
频数 |
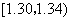 |
 |
 |
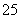 |
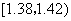 |
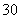 |
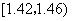 |
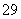 |
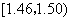 |
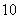 |
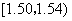 |
 |
| 合计 |
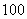 |
(1)列出频率分布表,并画出频率分布直方图;
(2)估计纤度落在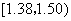 中的概率及纤度小于
中的概率及纤度小于 的概率是多少?
的概率是多少?
(3)从频率分布直方图估计出纤度的众数、中位数和平均数.
已知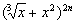 的展开式的二项式系数和比
的展开式的二项式系数和比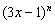 的展开式的系数和大992,求
的展开式的系数和大992,求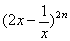 的展开式中:①二项式系数最大的项;②系数的绝对值最大的项。
的展开式中:①二项式系数最大的项;②系数的绝对值最大的项。
已知 ,其中
,其中 是自然常数,
是自然常数,
(1)讨论 时,
时,  的单调性、极值;
的单调性、极值;
(2)是否存在实数 ,使
,使 的最小值是3,若存在,求出
的最小值是3,若存在,求出 的值;若不存在,说明理由.
的值;若不存在,说明理由.
已知 在区间[0,1]上是增函数,在区间
在区间[0,1]上是增函数,在区间 上是减函数,又
上是减函数,又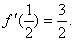 .
.
(1) 求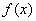 的解析式;
的解析式;
(2) 若在区间 (m>0)上恒有
(m>0)上恒有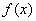 ≤x成立,求m的取值范围。
≤x成立,求m的取值范围。
已知抛物线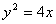 及点
及点 ,直线
,直线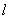 斜率为1且不过点
斜率为1且不过点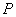 ,与抛物线交于点A,B,
,与抛物线交于点A,B,
(1) 求直线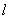 在
在 轴上截距的取值范围;
轴上截距的取值范围;
(2) 若AP,BP分别与抛物线交于另一点C、D,证明:AD,BC交于定点.