△ABC沿着BC方向平移,如图:B与C重合,C与D重合,A与E重合,已知△AB的面积为3。求△ABC平移过程中扫过的面积?
(本题8分)双休日,甲、乙、丙三人去A、B两超市购物,如果三人去A、B两超市的机会均等.(1)用画树状图的方法(或枚举法)表示出三人去超市的所有等可能结果;
(2)求出一人去A超市两人去B超市的概率.
(本题8分)先化简:
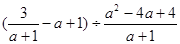 ,并从0,
,并从0,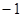 ,2中选一个合适的数作为
,2中选一个合适的数作为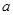 的值代入求值.
的值代入求值.
(本题满分12分)学完二次函数后,同学们对二次函数的图象抛物线产生了浓厚兴趣,在一次数学实验课上,孔明同学用一把宽3 cm且带刻度的矩形直尺对抛物线进行了如下测量:
①量得OA=3 cm;
②把直尺的左边与抛物线的对称轴重合,使得直尺左下端点与抛物线的顶点重合(如图①),测得抛物线与直尺右边的交点C的刻度读数为4.5.
请完成下列问题:
(1)求抛物线的对称轴.
(2)求抛物线所对应的函数关系式.
(3)将图中的直尺(足够长)沿水平方向向右平移到点A的右边(如图②),直尺的两边交x轴于点H、G,交抛物线于点E、F.求证:S梯形EFGH=
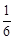 (EF2-9).
(EF2-9).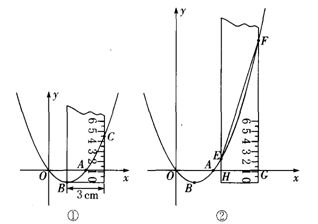
(本题满分12分)在四边形ABCD中,AD=a,CD=b,点E在射线BA上,点F在射线BC上.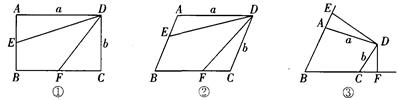
观察计算:
(1)如图①,若四边形ABCD是矩形,E是AB的中点.F是BC的中点,则四边形DEBF的面积S四边形DEBF=_______.
(2)若四边形ABCD是平行四边形,E是AB的中点,F是BC的中点,则S四边形DEBF:S四边形ABCD=_______.
(3)如图②,若四边形ABCD是平行四边形,且BE:AB=2:3,BF:BC=2:3,则S四边形DEBF:S四边形ABCD=_______.
探索规律:
如图③,在四边形ABCD中,若BE:AB=n:m,BF:BC=n:m,试猜想S四边形DEBF:S四边形ABCD=_______,请说明理由.
解决问题:
如图④,某小区角落有一四边形空地,为了充分利用空间,美化环境,想把它沿两侧墙壁改造为一块绿地,使绿地面积是原空地面积的3倍.请分别在两侧墙壁上确定点E、F,画出改造线DE、DF,并写出作法.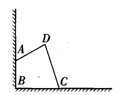
(本题满分10分)有3张不透明的卡片,除正面写有不同的数字外,其他均相同.将这三张卡片背面朝上洗匀后,第一次从中随机抽取一张,并把这张卡片上标有的数字记为一次函数关系式中的k,第二次从余下的两张卡片中再随机抽取一张,将上面标有的数字记为一次函数关系式中的b.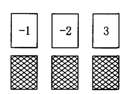
(1)写出k为负数的概率.
(2)求一次函数y=kx+b的图象经过第二、三、四象限的概率(用画树状图或列表的方法求解).