(
已知椭圆的两个焦点 ,且椭圆短轴的两个端点与
,且椭圆短轴的两个端点与 构成正三角形.
构成正三角形.
(1)求椭圆的方程;
(2)过点(1,0)且与坐标轴不平行的直线 与椭圆交于不同两点P、Q,若在
与椭圆交于不同两点P、Q,若在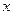 轴上存在定点E(
轴上存在定点E( ,0),使
,0),使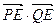 恒为定值,求
恒为定值,求 的值.
的值.
(本小题满分14分)已知函数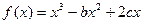 的导函数的图象关于直线
的导函数的图象关于直线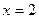 对称。
对称。
(1)求b的值;(2)若函数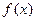 无极值求c的取值范围;(3)若
无极值求c的取值范围;(3)若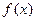 在
在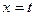 处取得极小值,记此极小值为
处取得极小值,记此极小值为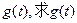 的定义域和值域。
的定义域和值域。
(本小题满分12分)已知椭圆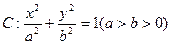 的长轴长为4。(1)若以原点为圆心、椭圆短半轴为半径的圆与直线
的长轴长为4。(1)若以原点为圆心、椭圆短半轴为半径的圆与直线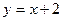 相切,求椭圆焦点坐标;(2)若点P是椭圆C上的任意一点,过原点的直线L与椭圆相交于M,N两点,记直线PM,PN的斜率分别为
相切,求椭圆焦点坐标;(2)若点P是椭圆C上的任意一点,过原点的直线L与椭圆相交于M,N两点,记直线PM,PN的斜率分别为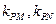 ,当
,当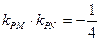 时,求椭圆的方程。
时,求椭圆的方程。
(本小题满分12分)将一个质地均匀的正方体(六个面上分别标有数字0,1,2,3,4,5)和一个正四面体(四个面分别标有数字1,2,3,4)同时抛掷1次,规定“正方体向上的面上的数字为a,正四面体的三个侧面上的数字之和为b”。设复数为 (1)若集合
(1)若集合 ,用列举法表示集合A;(2)求事件“复数在复平面内对应的点
,用列举法表示集合A;(2)求事件“复数在复平面内对应的点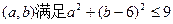 ”的概率。
”的概率。
(本小题满分12分)如图:已知正方体ABCD—A1B1C1D1,过BD1的平面分别交棱AA1和棱CC1于E、F两点。(1)求证:A1E=CF;(2)若E、F分别是棱AA1和棱CC1的中点,求证:平面EBFD1⊥平面BB1D1。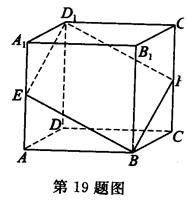
(本小题满分12分)已知函数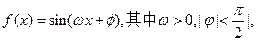
 ,且
,且 ,又知函数
,又知函数 (1)求
(1)求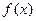 的解析式;
的解析式;
(2)若将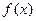 的图象向右平移
的图象向右平移 个单位得到
个单位得到 的图象,求
的图象,求 的单调递增区间。
的单调递增区间。